【9】例子--1--general--保序回归(Isotonic Regression)
这种回归,是这一种单调函数的回归,回归模型中后一个x一定比前一个x大,也就是有序,具体的数学公式在上面两个网址中都有。 保序回归并不需要制定的目标函数。保序回归的应用之一就是用来做统计推断,比如药量和毒性的关系,一般认为毒性随着药量是不减或者递增的关系,借此可以来估计最大药量。
一.数学定义
略
二、算法过程说明
从该序列的首元素往后观察,一旦出现乱序现象停止该轮观察,从该乱序元素开始逐个吸收元素组成一个序列,直到该序列所有元素的平均值小于或等于下一个待吸收的元素。
举例:
原始序列:<9, 10, 14>
结果序列:<9, 10, 14>
分析:从9往后观察,到最后的元素14都未发现乱序情况,不用处理。
原始序列:<9, 14, 10>
结果序列:<9, 12, 12>
分析:从9往后观察,观察到14时发生乱序(14>10),停止该轮观察转入吸收元素处理,吸收元素10后子序列为<14, 10>,取该序列所有元素的平均值得12,故用序列<12, 12>替代<14, 10>。吸收10后已经到了最后的元素,处理操作完成。
原始序列:<14, 9, 10, 15>
结果序列:<11, 11, 11, 15>
分析:从14往后观察,观察到9时发生乱序(14>9),停止该轮观察转入吸收元素处理,吸收元素9后子序列为<14,9>。求该序列所有元素的平均值得12.5,由于12.5大于下个待吸收的元素10,所以再吸收10,得序列<14, 9, 10>。求该序列所有元素的平均值得11,由于11小于下个待吸收的元素15,所以停止吸收操作,用序列<11, 11, 11>替代<14, 9, 10>。
三、举例说明下面实验的原理
以某种药物的使用量为例子:
假设药物使用量为数组X=0,1,2,3,4….99,病人对药物的反应量为Y=y1,y2,y3…..y99 ,而由于个体的原因,Y不是一个单调函数(即:存在波动),如果我们按照药物反应排序,对应的X就会成为乱序,失去了研究的意义。而我们的研究的目的是为了观察随着药物使用量的递增,病人的平均反应状况。在这种情况下,使用保序回归,即不改变X的排列顺序,又求的Y的平均值状况。如下图所示:
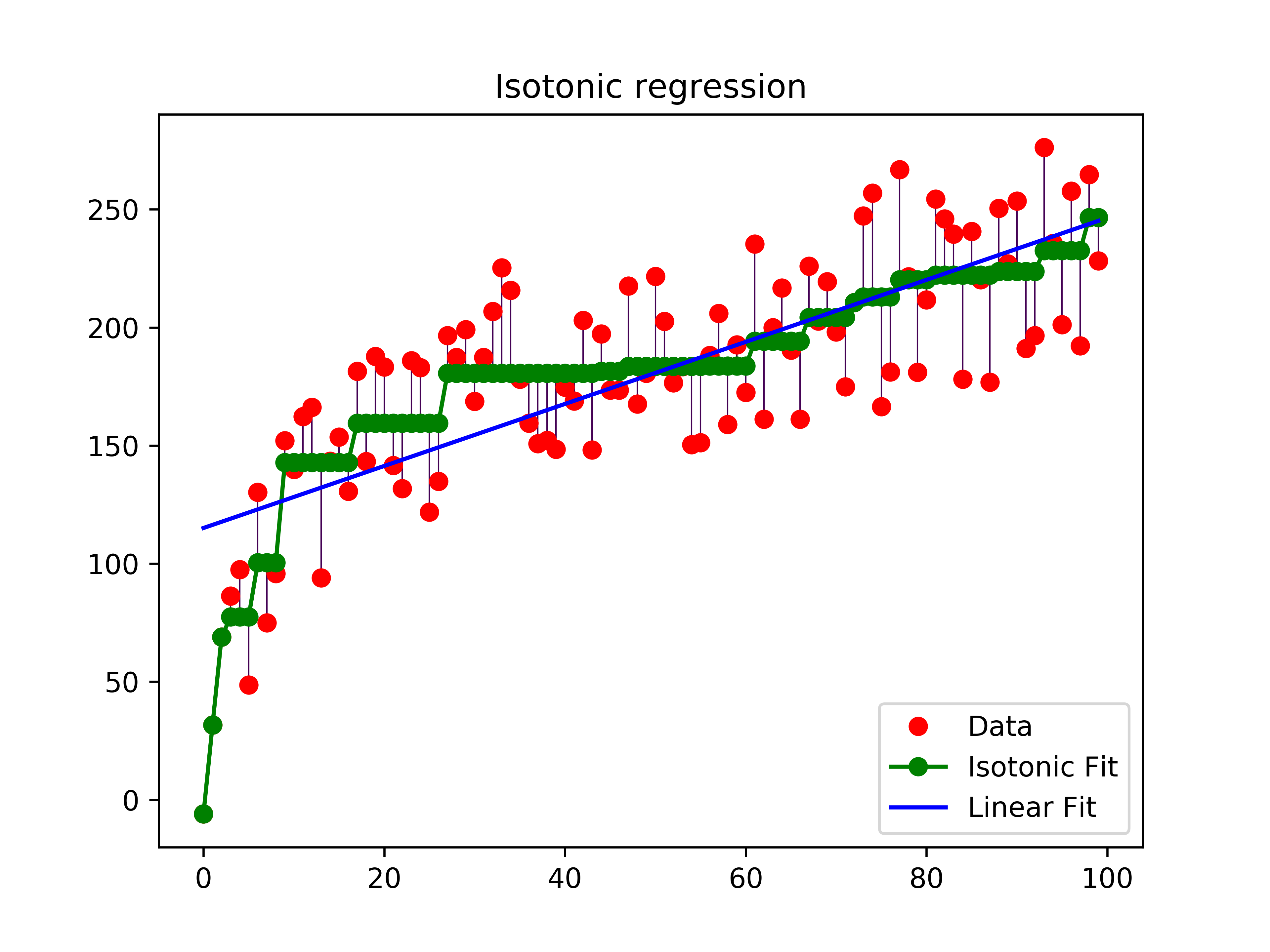
从图中可以看出,最长的绿线x的取值约是30到60,在这个区间内,Y的平均值一样,那么从经济及病人抗药性等因素考虑,使用药量为30个单位是最理想的。
当前IT行业虚拟化比较流行,使用这种方式,找到合适的判断参数,就可以使用此算法使资源得到最大程度的合理利用。
四、代码
print(__doc__)
# Author: Nelle Varoquaux <nelle.varoquaux@gmail.com>
# Alexandre Gramfort <alexandre.gramfort@inria.fr>
# License: BSD
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state
n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log(1 + np.arange(n))
ir = IsotonicRegression()
y_ = ir.fit_transform(x, y)
lr = LinearRegression()
lr.fit(x[:, np.newaxis], y) # x needs to be 2d for LinearRegression
segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(0.5 * np.ones(n))
fig = plt.figure()
plt.plot(x, y, 'r.', markersize=12)
plt.plot(x, y_, 'g.-', markersize=12)
plt.plot(x, lr.predict(x[:, np.newaxis]), 'b-')
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit', 'Linear Fit'), loc='lower right')
plt.title('Isotonic regression')
plt.savefig('isotonic_regression',dpi=600)
plt.show()
五、撸代码
1.rs = check_random_state(0)
主要是返回np.random.RandomState,避免每次随机出来的数字不一样。
2.rs.randint(-50,50,size=(n,3))
生成-50到50的n
[[ 41 -10 -14]
[ -2 -25 17]
[-15 -20 -21]
[-17 -32 -33]]
-
x[:,np.newaxis]
[[94] [95] [96] [97] [98] [99]]
把x编程了一个二维的数据(一个样本对应一系列feature)
type(np.newaxis)
NoneType
np.newaxis 在使用和功能上等价于 None,其实就是 None 的一个别名。 为numpy.ndarray(多维数组)增加一个轴
4.算法是个毛?
ir = IsotonicRegression()
y_ = ir.fit_transform(x, y)
lr.predict(x[:, np.newaxis])
lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)
5.segments那部分没看明白
参考资料:
http://blog.csdn.net/bea_tree/article/details/51009810
