【1.1】假设检验
一、假设检验的概念与原理
假设检验(hypothesis testing): 对总体的某种规律提出一个假设,通过样本数据推断,决定是否拒绝这一假设,这样的统计活动,称为 假设检验。
为啥有了零假设,我们还需要弄一个对应的备择假设呢?对备择假设的重要性,90多年前,英国著名的统计学家哥色特(其笔名就是Student)曾举例解释过这个问题,他的主要思想就是人们往往都倾向于选择相信概率比较大的事件。比如一些来自于正态总体的数据,现想检验它们的均值是不是等于a0?假设得到检验的概率值为0.0001,虽然这个值很小,但是你不能认为这批数据的均值不等于a0,为什么呢?因为这时候你只有一个a0供你检验,概率值再小,也不能否认它发生的可能性。而此时,如果你再有一个“备胎”(值为a1)让你去检验,最后检验的概率值为0.05,比前面的值大很多,这时候你就会倾向于选择后面a1这个值,而认为原来的a0不真。所以,我们需要有“比较”,多一个“备胎”,多一份选择!(此例子原型来源于《数理统计学简史》)。
二、假设检验的思维逻辑
例1 某市抽取400名小学生进行视力干预方法研究,干预组和对 照组各200人。研究前首先作基线调查,发现干预组屈光度的均 数为0.34D,标准差为0.12D;对照组屈光度的均数为0.57D, 标准差为0.36D。试问在基线时,干预组和对照组屈光度的总体均数有无差别?
样本均数分别为-0.34D和 -0.57D ,总体均数不等?
造成这种差别的原因可能有两种:
- 两总体均数相等 – 样本均数不同,乃抽样误差
- 两总体均数不相等 – 样本均数不同,并非抽样误差需进行假设检验!
三、假设检验的基本步骤
1.建立检验假设,确定检验水准:
- 零假设(null hypothesis),又称原假设,记为H0 ;干预组小学生和对照组小学生屈光度的总体均数相等 H0: µ1 =µ2 :
- 对立假设 (alternative hypothesis), 又称备择假设,记为H1 ;干预组小学生和对照组小学生屈光度的总体均数不等 Hsub>1 :µ1 ≠ µ2 (µ1 > µ2 ,µ1 < µ2 ) α = 0.05
2.选择并计算检验统计量
选择适宜的统计量
$$Z={\frac{\bar X_{1} - \bar X_{2}}{ \sqrt{\frac{S_{1}^2}{n_{1}} + \frac{S_{2}^2}{n_{2}}} }}$$
分子:样本均数之差 分母:样本均数之差的标准差 Z: 样本均数的差别(以其标准差为单位)
利用样本数据计算统计量的数值
$$Z={\frac{\bar X_{1} - \bar X_{2}}{ \sqrt{\frac{S_{1}^2}{n_{1}} + \frac{S_{2}^2}{n_{2}}} }} = {\frac{-0.34 - \left(-0.57\right) }{ \sqrt{\frac{0.12^2}{200} + \frac{0.36^2}{200}} }} = 8.57 $$
3. 确定Ρ 值,做出推断
Ρ 值:Ζ 的当前值之外的尾部面积

决策原则:H0成立时, 若当前情形是不太可能发生的,则拒绝H0
Ρ 值:Ζ 的当前值之外的尾部面积
Ρ 值的意义:在零假设成立的条件下,出现“统计量当前值及更 不利于零假设的数值”的概率为Ρ 。
- 若统计量当前值就拒绝零假设,则犯假阳性错误的概率为Ρ 。
- 规定一个“小”的概率 ,称检验水准(size of a test)
- 如果 P ≤ α ,表明“不大可能”犯假阳性错误;如果 P > a ,表明“颇有可能”犯假阳性错误
本例, Z=8.57, 查标准正态分布表, 得到 P<0.001 规定α=0.05 为“小”, P<α, 拒绝 H0,我们说“样本均数 的差异具有统计学意义”
可认为干预组和对照组小学生屈光度的总体均数不同。
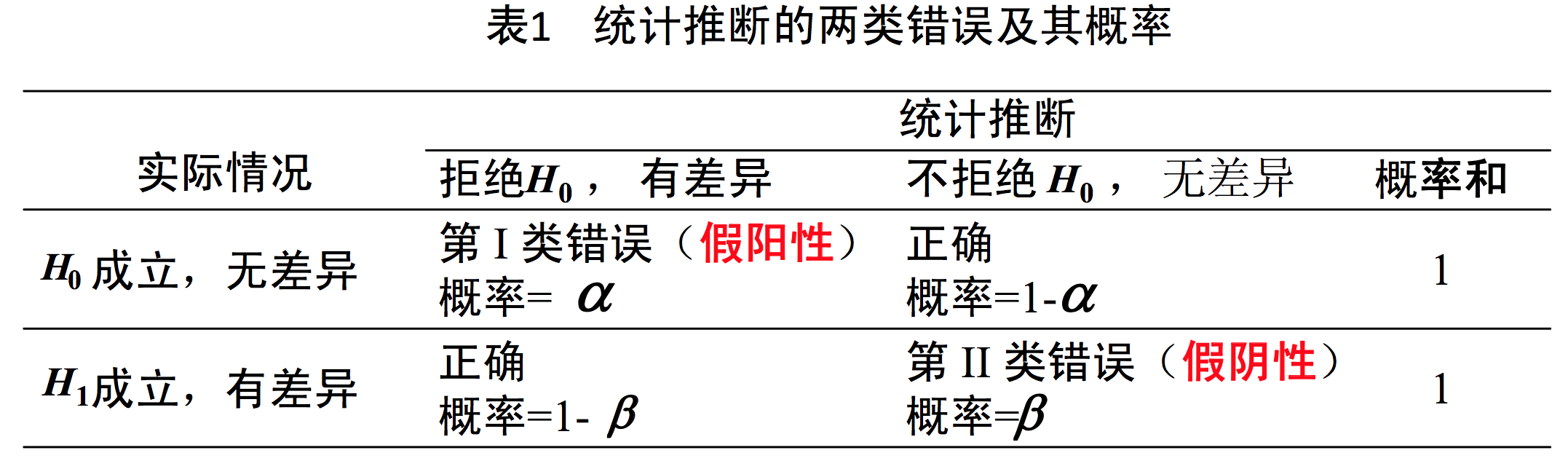
四、假设检验的两类错误
- 第 I 类错误 (type I error): 假阳性错误 例如,把没病说成有病,把无效说成有效等。
- 第 II 类错误(type II error):假阴性错误 例如,把有病说成没病,把有效说成无效等。
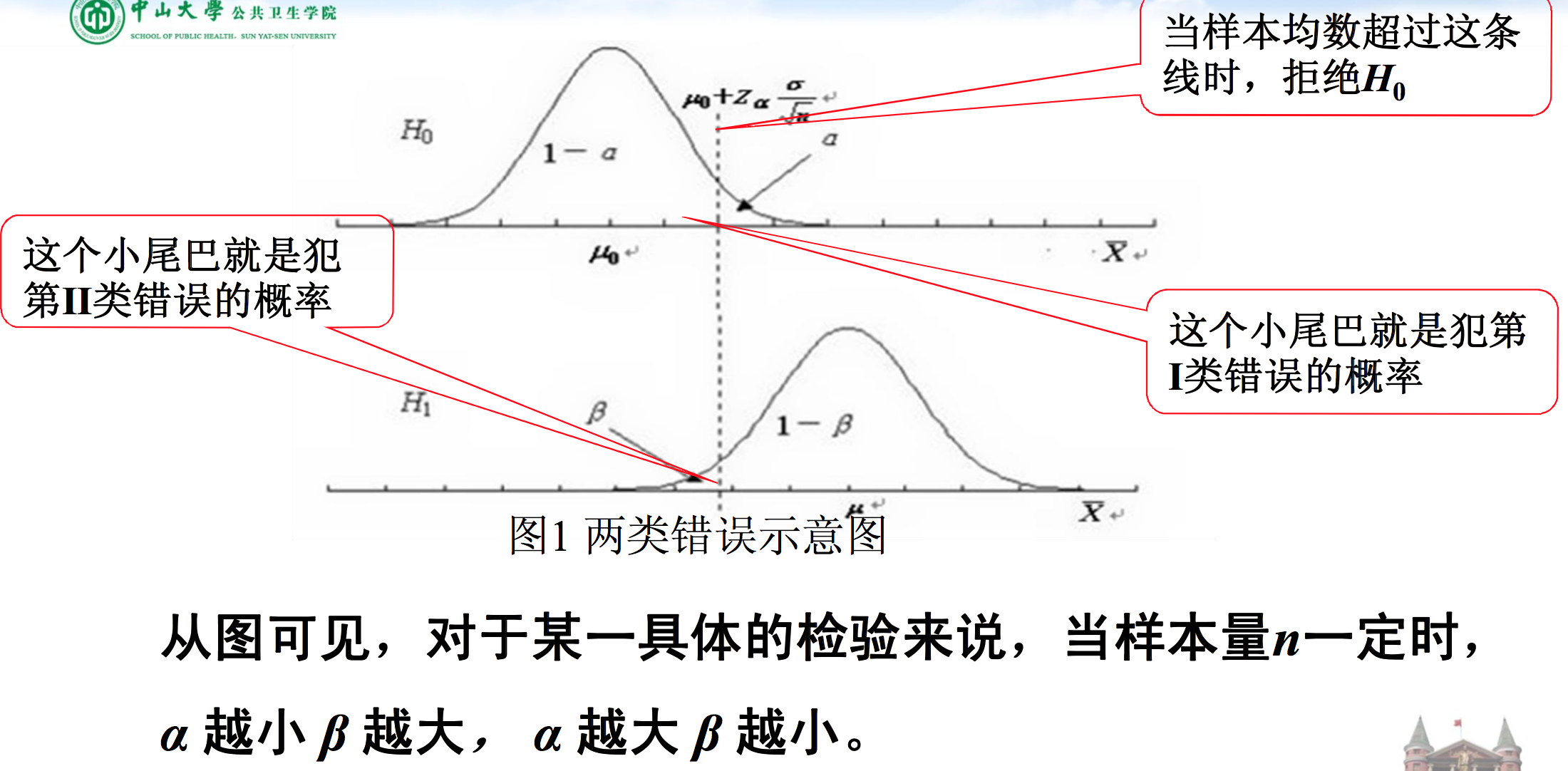
五、检验的功效
H0实际上不成立时,根据统计量的数值拒绝H0, 做对了! 这样的概率,称为检验功效 (power of test),记为 1 -β。
检验功效的意义:当两个总体参数的确存在差异时,所使用的统计检验能够发现这种差异的概率。
例 如果1 - β = 0.90,则意味着当H0实际上不成立时,理论上在每100次检验中,平均有90次能拒绝H0 。
1. 单样本设计资料 t 检验的功效
例1 已知北方地区一般儿童前囟门闭合月龄的均值为14.1,某研究人员从东北某缺钙地区抽取36名儿童,得前囟门闭合月 龄均值为14.3,标准差为5.08。问该县儿童前囟门闭合月龄是否大于一般儿童的前囟门闭合月龄?
经 t 假设,得 t =0.236,P >0.05,不拒绝H0。
可能的确和一般地区没差别; 但也可能样本量小, 功效不够大 ?!
试计算该检验的功效1-β
$$Z_{\beta} = \frac{\sqrt{n}\delta }{\sigma} - Z_{\alpha}$$
- n : 样本量
- δ : 欲发现的最小差异(或容许误差)
- σ : 总体标准差;
- Zα : 标准正态分布的临界值。 单侧检验时取单侧临界值; 双侧 检验时取双侧临界值
- Zβ : 标准正态分布的单侧临界值
算得 Zβ后,反查标准正态分布表来确定 β,进而得到 1-β
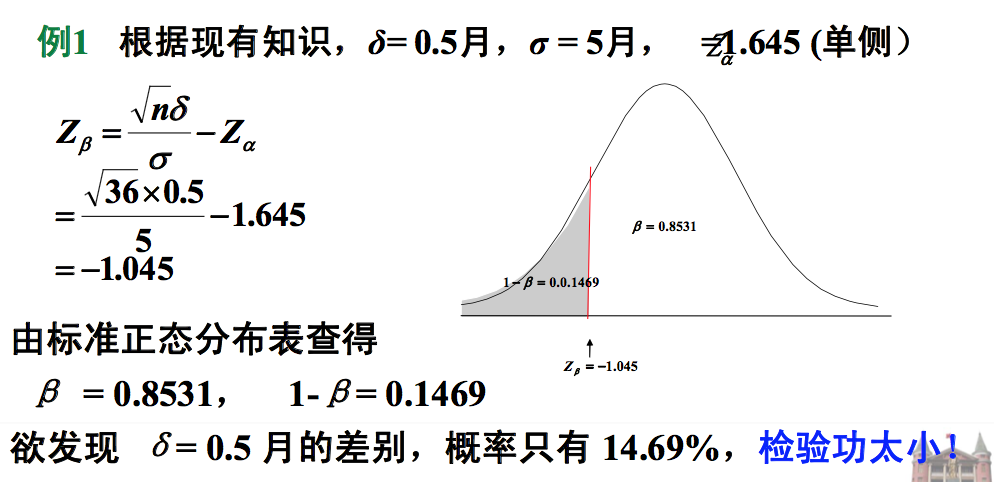
影响检验功效的主要因素:
- 参数间差异越大,功效越大
- 个体差异越小,功效越小
- 样本量越大,功效越大
- α越大,功效越大
在假设检验结果的解释和评价中,特别是分析 那些未能拒绝 H0 的假设检验结果,事后估计 1-β 的值, 有助于判断是总体的参数确实没有差别,还是由于样 本量太小,而导致检验效能不足,如1-β < 80%。
应用假设检验需哟啊注意的问题
- 应用假设检验必须符合其适用条件。
- 当样本量一定时,第I类错误的概率α小,第II类错误的概率 β 就大。反之亦然。
- 要正确理解 P 值的意义。P 值很小时,“拒绝H0,接受H1”,但不能理解为“很小的P 值说明总体参数间差异很大”。 P 值很小只是说明:“犯第I类错误的机会小”。
参考资料
