【5.4.1】Bray-Curtis similarity index（俩群落的相似性）

一、Bray-Curtis

Bray-Curtis距离是以该统计指标的提出者J. Roger Bray和John T. Curtis的名字命名的，主要基于OTUs的计数统计，比较两个群落微生物的组成差异。与unifrac距离，包含的信息完全不一样；相比于jaccard距离，Bray-Curtis则包含了OTUs丰度信息。

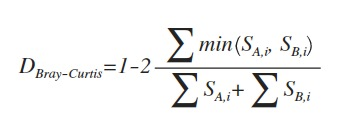
其中S_(A,i)和S_(B,i)表示第i个OTU分别在A群落和B群落中的计数。min表示取两者最小值。

举例说明

群落A和群落B的OTU统计如下表

community	OTU1	OTU2	OTU3	OTU4	OTU5
A	10	8	4	1	1
B	7	3	8	4	0
min(S_(B,i)S_(B,i)) = 7+3+4+1+0 = 15

sum(S_(A,i)) = 10+8+4+1+1 = 24
sum(S_(A,i)) = 7+3+4+8+4+0 = 22

D = 1 - 2*15/(24+22) = 0.3478

当然，D值越小越好，表示二者组成差异小。

二、R的实现

vegdist {vegan}

Bray-Curtis similarity index

vegdist(x, method="bray", binary=FALSE, diag=FALSE, upper=FALSE,na.rm = FALSE, ...)

各种方法介绍：

euclidean d[jk] = sqrt(sum(x[ij]-x[ik])^2)

binary: sqrt(A+B-2*J)

manhattan       d[jk] = sum(abs(x[ij] - x[ik]))

binary: A+B-2*J

gower       d[jk] = (1/M) sum(abs(x[ij]-x[ik])/(max(x[i])-min(x[i])))

binary: (A+B-2*J)/M,

where M is the number of columns (excluding missing values)

altGower d[jk] = (1/NZ) sum(abs(x[ij] - x[ik]))

where NZ is the number of non-zero columns excluding double-zeros (Anderson et al. 2006).

binary: (A+B-2*J)/(A+B-J)

canberra  d[jk] = (1/NZ) sum ((x[ij]-x[ik])/(x[ij]+x[ik]))

where NZ is the number of non-zero entries.

binary: (A+B-2*J)/(A+B-J)

bray          d[jk] = (sum abs(x[ij]-x[ik]))/(sum (x[ij]+x[ik]))

binary: (A+B-2*J)/(A+B)

kulczynski         d[jk] 1 - 0.5*((sum min(x[ij],x[ik])/(sum x[ij]) + (sum min(x[ij],x[ik])/(sum x[ik]))

binary: 1-(J/A + J/B)/2

morisita   d[jk] = 1 - 2*sum(x[ij]*x[ik])/((lambda[j]+lambda[k]) * sum(x[ij])*sum(x[ik])), where

lambda[j] = sum(x[ij]*(x[ij]-1))/sum(x[ij])*sum(x[ij]-1)

binary: cannot be calculated

horn Like morisita, but lambda[j] = sum(x[ij]^2)/(sum(x[ij])^2)

binary: (A+B-2*J)/(A+B)

binomial   d[jk] = sum(x[ij]*log(x[ij]/n[i]) + x[ik]*log(x[ik]/n[i]) - n[i]*log(1/2))/n[i],

where n[i] = x[ij] + x[ik]

binary: log(2)*(A+B-2*J)

cao   d[jk] = (1/S) * sum(log(n[i]/2) - (x[ij]*log(x[ik]) + x[ik]*log(x[ij]))/n[i]),where S is the number of species in compared sites and n[i] = x[ij] + x[ik]

参考资料：

• http://cc.oulu.fi/~jarioksa/opetus/metodi/sessio3.pdf
• https://blog.csdn.net/zhihaoyi/article/details/90480003