【4.1】隐马尔可夫模型建立预测模型
一、从状态到马尔可夫链
前面我们提到了空位罚分的原则,那里面我们是将产生gao open和gap exending 等同来看的,但是gap 和gap extending 应该区分来看待,分别给予不同的罚分:
Penalty = d + (n-1)*e
在计算的过程中,要想区分gap open和gap extending ,我们需要引入状态的概念,也就是需要记住之前是否open 了一个gap.之前我们也提到两条序列比对的过程中,两条序列中需要比对的两个碱基X,Y,要么比对上,可以是不完全比对上,要么X对上空格,要么Y对上空格。如下图
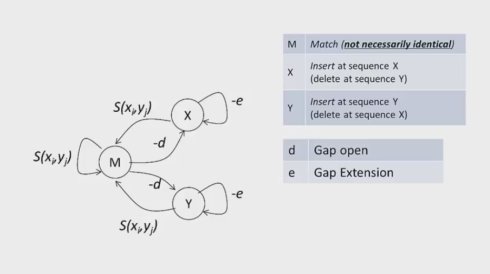
当我们将gap extending考虑进来,算法就如下罗,M(i,j)是横左边为i,纵坐标为j时,那个方格子里面最高的分数(总分数),它来源三种情况。一次类推。

跟之前的F相似,我们用动态规划矩阵,将三组转化关系表示在三个平面间的填充,只是对于每一个平面而言,回溯关系既可能来自本平面,也可能来自另外一个平面,或者说另外一个状态,我们构造一个马尔可夫链(由俄国数学家,一个基于概率的随机过程模型,用于刻画一组存在关联的随机事件)

马尔可夫链:A Markov chain describes a discrete stochastic process at successive times. The transitions from one state to all other states, including itself, are governed by a probability distribution。(用于描述一组弥散状态间在不同时刻的转移关系,值得注意的是,这里的转移关系不需要是已确定的,只需要由一个概率分布描述即可。唯一的要求是t时刻的状态分布又且只由之前有限个m时刻状态分布概率来确定,称为m阶马尔可夫链)
事实上,我们通常只考虑最简化的情形,1阶马尔可夫链,当前的状态且只于前一个状态相关。我们引入转移概率的概念。在t时刻从k态转移到l态的概率,并构成一个转移矩阵,从定义上我们知道这个矩阵沿对角线不是对称的。

通常,我们会假定这个转移概率与t无关,也就是所谓的齐次马尔可夫链,这也刚好是我们线性组合罚分的情形。我们对每一种可能的延伸分配一个概率。首选考虑M到X,Y,也就是gap open的概率,以及X,Y到自身,也就是gap extending的概率。然后我们可以得到其他的几个概率分布,从而得到完整的转移概率矩阵。我们可以简单的根据乘法定理来计算出任何一个比对的概率值。比如如下图的这个例子,我们将相应的概率依次乘起来,就可以得到对应的概率值。事实上,我们可以对任意比对计算出概率值,也就是说我们通过引入马尔可夫链,给出了序列的概率解释
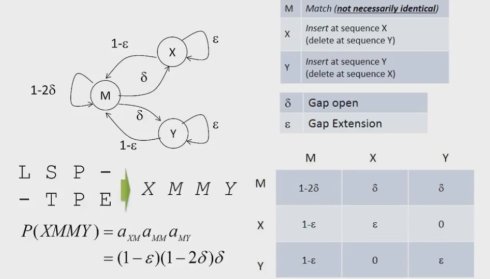
马尔可夫链几个问题?
- There isn’t direct transition between X and Y in our model, do you think it’s reasonable?
- Is it possible to have global alignment based on the rephrased Markov Chain‐based model?
二、隐马尔可夫链
前面我们说道通过引入状态的概念,我们来区分gap open和gap extending,来完成线性组合空位罚分,并对任意比对计算出概率值。但仅靠这些还不能真正完成序列比对,因为现有的模型只是区分了空位X,Y状态,以及M状态,而没有考虑具体的残基,因此我们需要进一步引入隐马尔可夫模型。
所谓隐马尔可夫模型(Hidden Markov Model),在状态的基础上增加了符号(token)的概念,每个状态都可以以不同的概率产生(emit)一组可以观察到的符号。
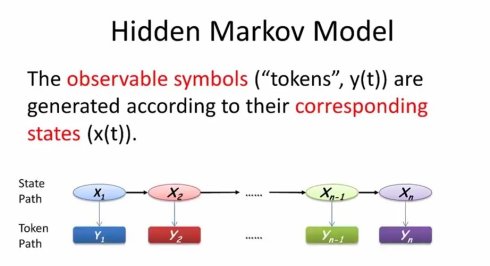
也就是说,除了状态转移概率之外,隐马尔可夫模型进一部引入了“生成概率”(emission probability)的概念,每个状态都有自己的生成概率分布,可以按照不同的概率产生一组可以被观测到的符号。与上一节不同,隐性马尔可夫模型的状态路径是无法直接看到的。这也是Hidden Markov Model中Hidden的含义。相反,我们需要根据观察到的符号,来推测对应的状态。
例如,当我们观测到字符串aabc时,对应的状态路径有可能是1123,也有可能是1233,或者1333,或1111,2222,3333等等(不明白)。因为每个状态都有可能产生abc.问题是不同状态产生abc的概率不一样,进而不同的状态路径最后产生的观测到的字符串aabc的概率也不同。理论上,我么可以把所有的路径穷举出来,每一个都可以算出路径概率,然后取概率最大的,就是我最可能的路径。。
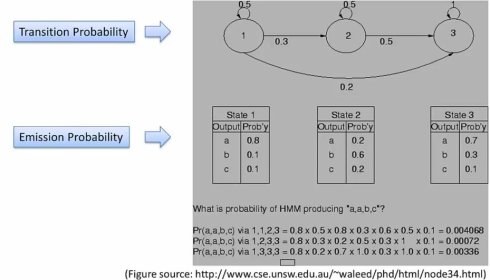
我们在上一节定义的转移概率,再定义一个生成概率,ek(b)表示状态为Sk的时候b的概率,这样我们就能计算出状态路径的概率。

我们在考虑空位线性罚分模式的序列比对问题,之前提高,建立马尔可夫链通过引入空位状态X,Y以及Match状态M,可以很好处理gap open和gap extending,但没有考虑到具体的残基,因此,我们接下来通过引入刚刚介绍的隐形马尔可夫模型来补充这一点。
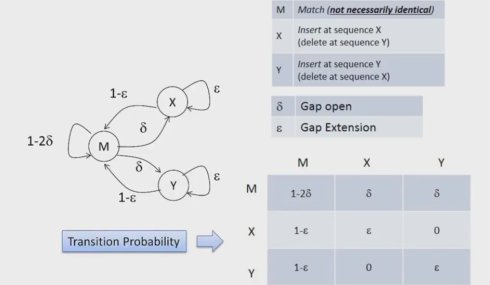
具体来说,我们用生成概率来处理残基,M状态生成的符号是所有可能的残基替代,其生成概率写作p a,b。而X和Y状态生成的符号则是所有可能插入的残基,其生成概率写作qa.这样,我们就可以很方便的具体考虑状态和具体的残基,并进而将序列比对问题重新描述为一个针对特定隐马尔可夫模型与符号串寻找最可能状态路径的问题。
我们定义PM(i,j)表示在Xi比对到Yj,也就是两个残基对在一起的时候,第一条序列X从第一位到i位,第二条序列Y从第1位到第j位的最大概率.而PX(i,j)和PY(i,j)分别表示在Xi或Yj残基比对到空位时,序列X从第1位到第i位,序列Y从第1位到第j位最大的概率。这样,我们就可以进一步根据状态转换图来定义每步的迭代函数,并进一步应用动态规划的back tracking来得到最终的比对。
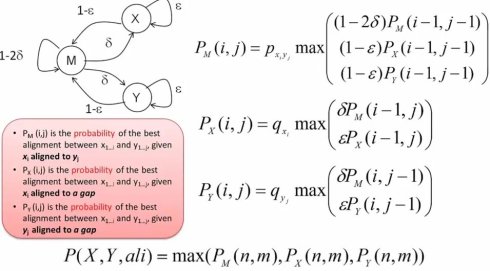
总结一下,我们通过引入隐马尔可夫模型,来解决序列比对中线性组合空位的问题 首先,隐马尔可夫模型的引入,有效的给出了序列比对的概率解释(probabilistic interpretation),比如,之列的delta就可以理解为在生物演化过程中,出现DNA片段插入或删除的概率,或者说,产生一个空位问题。再比如,M状态的生成概率,就可以直接地对应于演化过程汇总相应替代发生的概率。
同时,概率模型的引入,可以帮助我们利用该理论的知识做更多的分析。例如,我们可以在不引入具体比对的情况下,计算两条序列之间最大可能的相似性。
在隐马尔可夫模型中,同一观察序列可以来自许多不同的状态路径,因此,我们将所有可能状态路径对应的概率求和时,我们就得到了相应观察序列对应的全概率(full probability)。在序列比对这个问题上,也就是两条序列之间爱你所有可能的比对概率之和。或者说,两条序列之间最大可能的相似性。
在具体操作撒谎那个,我们只要将之前每一步迭代时求最大值变为求和。再将求最大值变为求和就可以了。

因为这个方法是将所有可能的概率求和,他不依赖于特定的比对,对于之前提到的多个最优比对的情形,尤其重要。隐马尔可夫模型通过符号观测序列来反推状态。在应用领域,他并不局限于序列比对。事实上,在现代生物信息学的研究中,隐马尔可夫模型更多的是被用作一个预测器。
三、用隐马尔可夫模型建立预测模型
我们前面说道,隐马尔可夫模型中状态与观测相分离的特点,这使得同一个观测到的额符号序列,可能来自多个不同的状态路径。每个状态都有自己的生成概率分布,按照不同的概率产生一组可以被观测到的符号,从而使观测到的符号学列去反推其对应的状态路径成为可能。
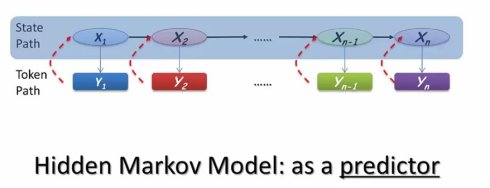
具体来说,我们可以对每个可能的状态路径,计算其产生观测符号串的可能性,而其中概率最大的那个状态路径,也就是最可能产生这个字串的路径。
接下来,我们来做一个最简单的基因预测。给定一段基因组DNA序列,我们来预测其中的编码区。按照之前说道的隐马尔可夫模型,我们先要区分不能直接观测到的隐状态和可以直接观测的显符号。

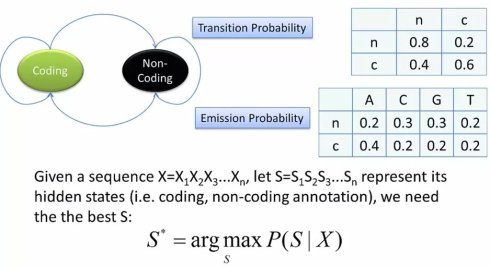
在这个例子里,我们可以很容易看出,给定的基因组DNA序列是可以观测到的符号串。而编码/非编码是不能直接观测的隐状态。因此,我们可以画出状态转换图。首先我们有编码和非编码两个状态。因为基因组会同时包好编码和非编码区域,因此这两个状态之间可以转换。当然,每个状态也可以转换到自己,表示连续的编码或非编码区域。这样,我们就有了一个2*2的转移矩阵,也就是alpha,k,l
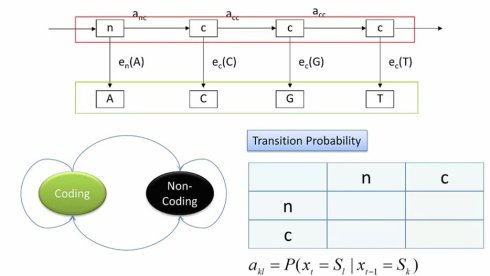
接下来,我们需要写生成概率,也就是e,k,b。这个也很直观,无论是编码还是非编码状态,都有可能产生A,C,G,T四个碱基,因此我们由可以分别有两个矩阵。
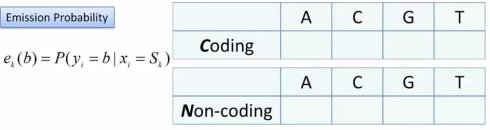
现在,我们需要一个训练集(Training set),来把这三个矩阵的格子中填上具体的数值。具体来说,我们需要一个已经事先注释过得——也就是说正确标记了编码,非编码区域的DNA序列,通常这个序列要比较长,以便有充足的数据统计。

假定我们经过训练集的分析,分别填好了转移矩阵概率和生产概率矩阵。我们需要根据这些数据,来对一个未知的给定基因组序列反推出最可能的状态路径,也就是概率最大的那个状态路径。因此,我们还是和之前一样利用动态规划的算法,写出迭代公式,以及最后的终止点公式(Termination equation)
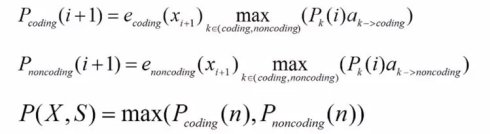
从公式里面,我们看到,我们需要做大量测乘法。这个不仅比较慢,而且利用计算机操作时,随着连乘次数的增加,很容易数值过小而出现下溢(underflow)的问题。因此,我们通常会引入对数计算,从而将乘法转换成加法。具体来说,就是对转移和生成概率都预先去log10。

好,我们正式开始 CGAAAAAATCG
首先,让我们和之前一样,画出动态规划的迭代矩阵,其中包含两个状态,非编码状态n与编码状态c。接下来,我们需要设定边界条件(boundary condition),也就是这两个状态默认的分布比例。为了计算方便,我们分别设为0.8和0.2,经过log10转换后,分别为-0.097和-0.699.接下来我们逐步填格子
首先,我们碰到的第一个符号C,由生成概率可以知道,他在非编码状态下的log10生成的概率是-0.523,将之与-0.097相加,就可以得到-0.62类似的,在编码状态下,这个数是-0.699+(-0.699)=-1.4。接下来我们要前进一个碱基,就需要进行状态转移,我们先来看第一种情形,也就是从非编码状态到非编码状态的转换。从转移举证可以看到,这里的转移概率是-0.097,再加上非编码状态下下一个碱基G的生产概率是-0.523.我们能就可以得到-1.24。类似的我们来计算,在这个位点从编码状态到非编码状态的转换,也就是-1.40+(-0.398)+(-0.523)=-2.32.这个值比从非编码状态转移得到的-1.24小,因此不会被保留。类似的,我们可以继续完成后续的迭代,把后面所有的格子都一个个填满。
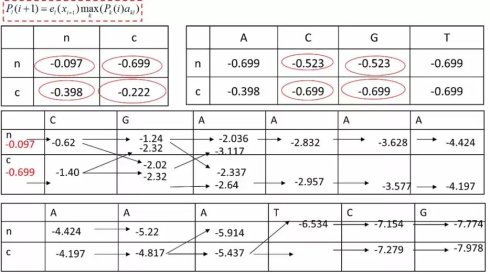
接下来,我们来做回溯。首先,选出最终概率值最大的那个值。以他为起点,一次来回溯,那么我们拿到的回溯路径,就可以得到最终的结果。
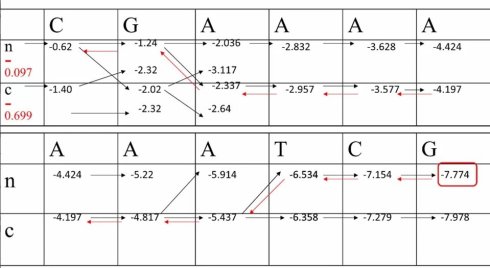
我们就可以得到最后的结果,NNCCCCCCNNN,也就是说,我们把输入的序列CGAAAAAATCG分为了非编码区N和编码区C.
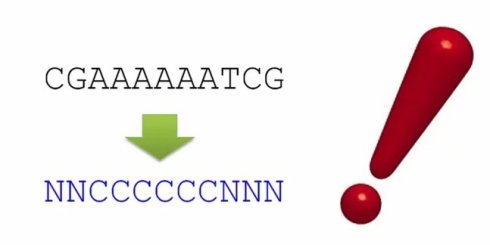
由于时间有限,我们的MSGP(The Most Simple Gene Predictor)非常简单。但它很容易被扩展,只需要你引入更多的状态,唯一的限制是,不同的状态对应的生成概率–在这里也就是碱基的组分–必须存在显性的差异。这样,我们才可能由你的观测序列反推出状态来。
比如说,Chris Burge 1996年提出基因预测算法GenScan针对外显子,内含子以及UTR等设定了独立的状态,从而大大提高了预测的准确度,是最成功的基因预测工具之一。但在基本原理上,它与我们刚刚敬爱那个过,最简单的MSFP并没有区别。类似的,我们还以可以哟娜类似的方法去做5’剪切位点的预测等等。
事实上,通过将状态和可观测的符号分离开,隐马尔可夫魔心为生物信息学的数据分析提供了一个有效的概率框架,是当代生物信息学最常用的算法模型之一。
参考资料:
北大高歌老师课件
