【4.6.1】序列预测抗体夹角-PAP(Packing Angle Prediction)
这是2010年发表的一个工具,现在来看,这个工具有了很多问题,但里面很多思想值得我们去借鉴,因此,把这篇文献的脉络给拎出来了。
目的:
抗体中VH和VL结构域的结合可以变化,从而影响抗原结合位点的几何形状。然而,直到最近,这在建模抗体结构中基本上被忽略了。 我们提出了对已知结构中观察到的变异程度的分析,以及用于预测结合角度的机器学习方法。
一、工具
1.1 网页版(PAPS)
输入一条重链,一条轻链,即可给算出夹角
http://www.bioinf.org.uk/abs/paps/
1.2 本地版 (PAPA)
cd /data/software
git clone https://github.com/ACRMGroup/papa.git
cd papa
./install.sh /bin
本地版的存在两个问题:
1.输入序列需要有坐标信息,例如:
L1 Q
L2 V
L3 E
... etc ...
2.需要安装SNNS(一种神经网络建模的工具)
所以呢,本地的,我也没用。。。
二、原理介绍
PAP (Packing Angle Prediction) 这个工具对应的文献为《Analysis and prediction of VH/VL packing in antibodies》
简单梳理一下该工具,做了两件事情:
- 定义angle,并计算出561个PDB的angle
- 选择20个残基的feature,用于预测angle
涉及到的工具:
- FroFit 用于结构的fit
- AbNum 用于排序抗体序列(Chothia numbering)
- NACCESS 用于计算可溶性(Accessibility),将潜在的表面残基定义为由于VH / VL相互作用而溶剂可及性(solvent accessibility)发生任何变化的位置
2.1.定义angle
1.5个PDB的结构superposition,然后选择保守的位置,一共选了8个保守的残基(L35– L38, L85–L88, H36–H39, H89–H92),见图1;

2.给定的PDB结构,分别提取轻链和重链的8个保守残基Cα原子的坐标,形成数据集SL和SH。(L35– L38, L85 – L88, H36 – H39, H89 – H92)
3.计算出SL和SH的中心坐标CL和CH
4.PCA分析,分别找到经过CL和CH的能够很好fit的线 SL和SH
5.分别找到轻链和重链对应的线上的点 PL和PH, 这些点与各自的中心位点在同一侧
6.计算PL、CL、CH、PH所形成的扭转角,定义为为Packing angle
7.567个夹角(561个PDB ID)被计算出来,用于后续构建神经网络模型
2.2 神经网络的构建(Neural networks)
在一个全连接神经网络中需要的变量Nv为:
$$ N_{v} = (S_{i} * S_{h}) + (S_{h}*S_{o}) $$
- Sh 是隐藏层的节点数
- So 是输出层的节点数
- Si 是输入层的节点数 Si = Ni * Se
- Ni 是输入的个数,Se是encoding vector的大小
根据一般的经验法则,训练的数据集大小需要为3Nv ,尽管事件中,更小的训练数据集也有被用到。如果我们用124个潜在的表面残基,一个残基的encoding vector为20(用长度为20的0,1来代表残基,1所在不同的位置代表不同的残基),则Si为2480. 如果我们隐藏节点为20,一个输出节点来代表packing angle,则Nv = 24810。 这远远超出了我们可用于训练的数据集。
为了减少输入数据,常规的用长度为20的encoding vector来代表一个残基的方法,被长度为4的描素物理化学性质的向量取代,包括:(i) the total number of side-chain atoms; (ii) the number of side-chain atoms in the shortest path from the Ca atom to the most distal atom; (iii) the Eisenberg consensus hydrophobicity (Eisenberg et al., 1982); (iv) the charge (his- tidine was assigned a charge of þ0.5).
因此,用20 (20个代表残基)* 4(每个残基的描素符)作为输入,10个节点的隐藏层,一个节点的输出,用Stuggart Neural Network Simulator (SNNS, http://www.ra.cs.uni-tuebingen.de/SNNS/)来构建神经网络。The Resilient Backpropagation (RProp) learning function (Riedmiller and Braun, 1993) was used for training the network.Training used early stopping after 150 cycles, or a sum-of-square error 1.5.
输出结果向量化
$$ θ_{f} = 1 - \frac{θ- θ_{min}}{ θ_{max} - θ_{min}} $$
- θf是interface angle fraction
- θ is the interface angle
- θmax and θmin 是观察到的最大和最小的interface angle
2.3. 选择用于构建预测angled的feature
基于GA(Genetic algorithms)算法,从124个表面残基(重链61,轻链63个)选取20个残基(10个重链,10个轻链)用于构建神经网络模型,根据预测结果的表现,不断迭代,直到选出最佳的表型模型(1-RELRMSE= 0.83)对应的20个残基 ,对应的残基为:L38, L40, L41,L44, L46, L87, H33, H42, H45, H60, H62, H91 and H105
3.3.1 Genetic algorithms
为了找出最能用于预测结构的表面残基,采用了GA算法
GA基于一个群体并迭代地重复三个步骤:
- 评估和选择最适合下一代父母的人
- 两个选定父母的配对
- 突变使后代的等位基因随机变化
群体中的个体由长度为124或64的二元向量组成(分别代表潜在表面的残基或framework 残基的总数)。 每个等位基因是1或0以指示表面残基是否包括在训练神经网络中。 任何个体只允许最多20个等位基因设置为1。
最初随机创建个体群体,并使用5倍交叉验证训练和验证神经网络的结果,评估每个个体的质量。 通过高分数个体的配对产生新的群体,然后以指定的速率(m)进行随机突变,默认值为m = 0.0001。 重复评估和产生新种群。
采用了“generational replacement”策略,其中整个父母群体被儿童取代,以允许快速探索表面位置。 记录每一代中最好的个体,以防最佳个体的适应性在后代中减少。
评估了两种最常见的选择父母的策略:轮盘选择(Roulette-wheel selection)和基于排名的选择(Roulette-wheel selection)。 轮盘赌选择是一种适应性比例选择方法,其中选择特定父母的可能性由父母的适合度除以群体的平均适合度给出。 在基于等级的选择中(Baker,1985),按照适应度对人口进行排名,选择以与轮盘赌计划类似的方式进行,但绝对分数由等级替换。 在任何一种情况下,在所选父母中随机选择交叉点,并将父母的两部分组合以产生后代。
这些方案的一个问题是人口的过早收敛。 最初,人口相当多样化,但是得分明显优于其他人的父母被更频繁地选择,因此可以导致相同的孩子。 当群体中多余个体的数量增加时,随机选择两个相同个体进行配对的机会也增加。 相同个体的交叉显然会产生与父母相同的孩子。 由于应用于后代个体的突变率非常低(μ = 0.0001),最终的后代可能不会改变。 然而,更高的突变率(μ = 0.001)无助于抑制冗余个体数量的指数上升(见结果,图5)
因此,我们开发了一种方法,其中使用基于秩的选择来选择父个体,但是突变率是动态变化的,这取决于为配对选择的父母的相似性。 我们称之为智能选择的方法如下所述:
- 对于要创建的每个孩子,根据基于排名的选择选择2个父母P1和P2
- 随机选择交叉点并拼接P1和P2以创建子Oi
- 计算父母P1和P2之间的相似度S(P1,P2)
$$ S(P1,P2) = 2 * \frac{ P1 n P2 }{|P1| + |P2|} $$
当两个父母完全一样的时候,相似性为1,当两者没有共同的残基的时候,相似性为0。然后根据相似性来调整突变频率
- if (0.9 ≤ S(P1,P2) ≤ 1.0), then swap five 0s and 1s in Oi
- if (0.7 ≤ S(P1,P2) < 0.9), then δ = 0.01
- if (0.5 ≤ S(P1,P2) < 0.7), then δ= 0.008
- if (0.3 ≤ S(P1,P2) < 0.5), then δ = 0.005
- if (0 ≤ S(P1,P2) < 0.15), then δ = 0.001
3.3.2 预测结果的评估
- 5-fold cross vali- dation
Pearson’s correlation coefficient
然而,Pearson的r在预测精度方面并不是对神经网络实际性能的非常直观的测量,并且不能很好地反映异常值的存在。 相对RMS误差(RELRMSE)(Masters,1993)计算误差的RMS值,并取该值与实际值的平方和之比
$$ RELRMSE = \sqrt{ \frac{\sum_{i=1}^{n}(x_{i}-p_{i})^{2}}{ \sum_{i=1}^{n} x_{i}^{2} }}$$
其中xi是实际的界面角度分数,pi是预测的界面角度分数。 由于RELRMSE是比率,因此它是无量纲值。 对于每个个体,RELRMSE计算5-fold,并且个体的得分计算为
SCORE = 1 - RELRMSE
从最初的性能统计数据(数据未显示)来看,RELRMSE似乎比Pearson的r或其他测量方法(如RMSE)对小packing angle和大packing angle的预测误差更敏感。
$$ RMSE = \sqrt{\sum_{i=1}^{n} \frac{(x_{i}-p_{i})^{2}}{n}}$$
因此,RELRMSE用于评估主要GA运行中的预测质量
2.4 结果
夹角的分布
567个PDB, Chothia编号
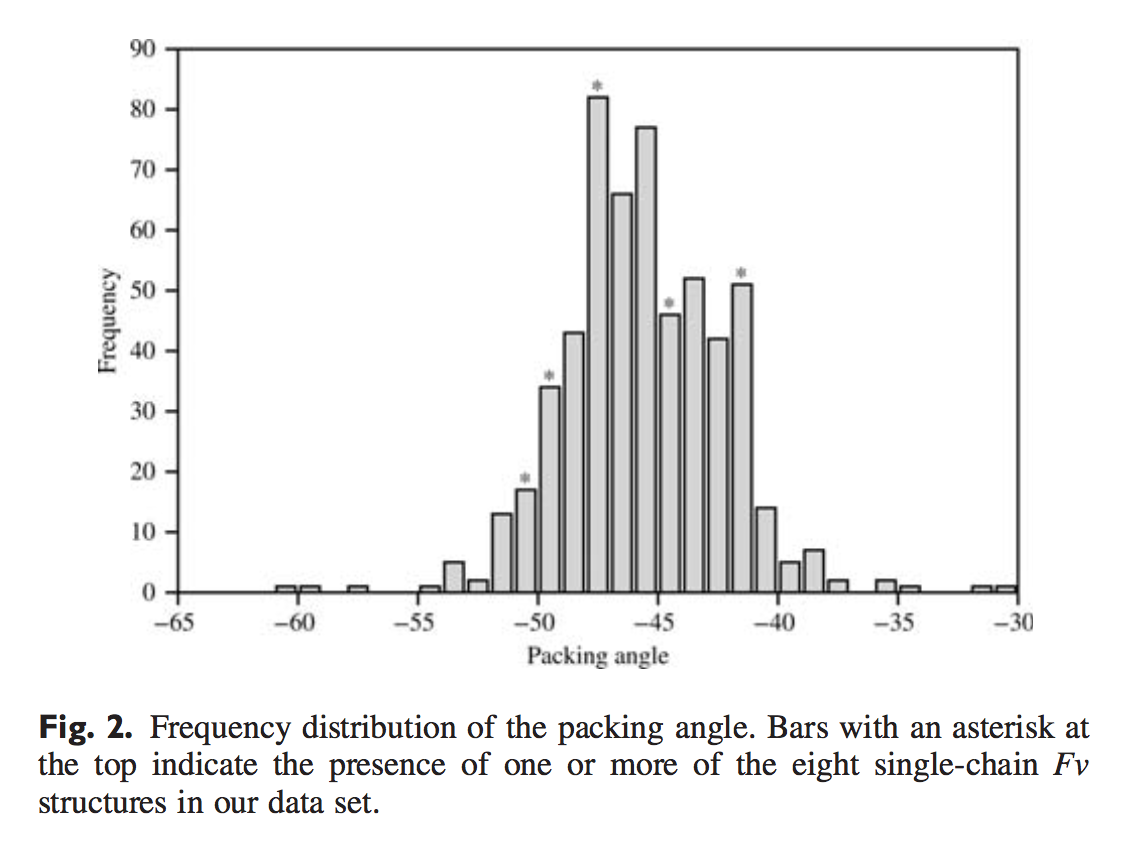
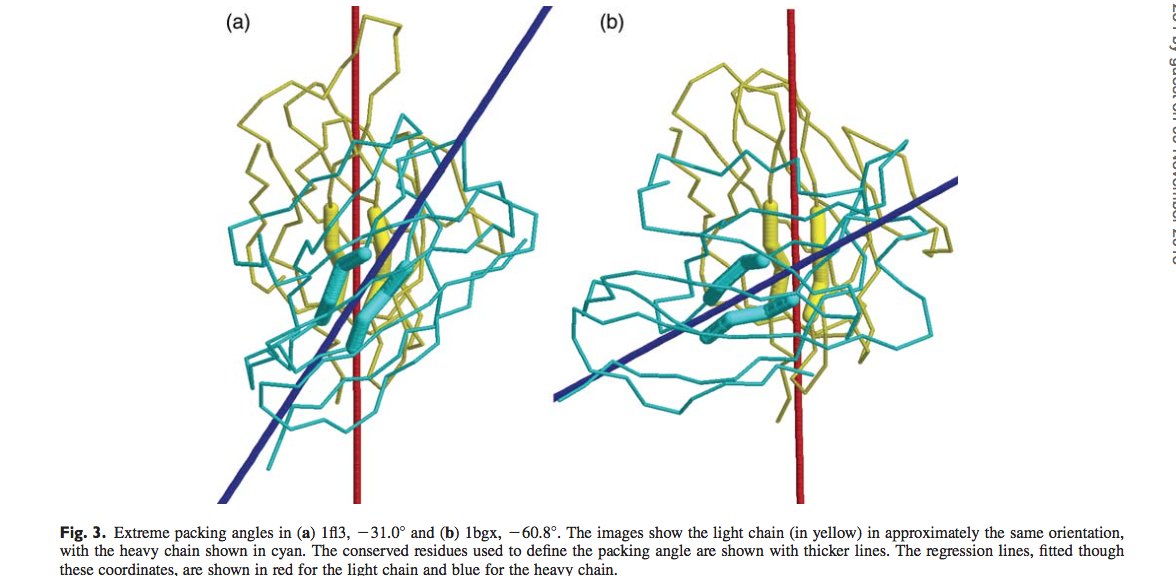
初步的通过表面残基预测packing angle
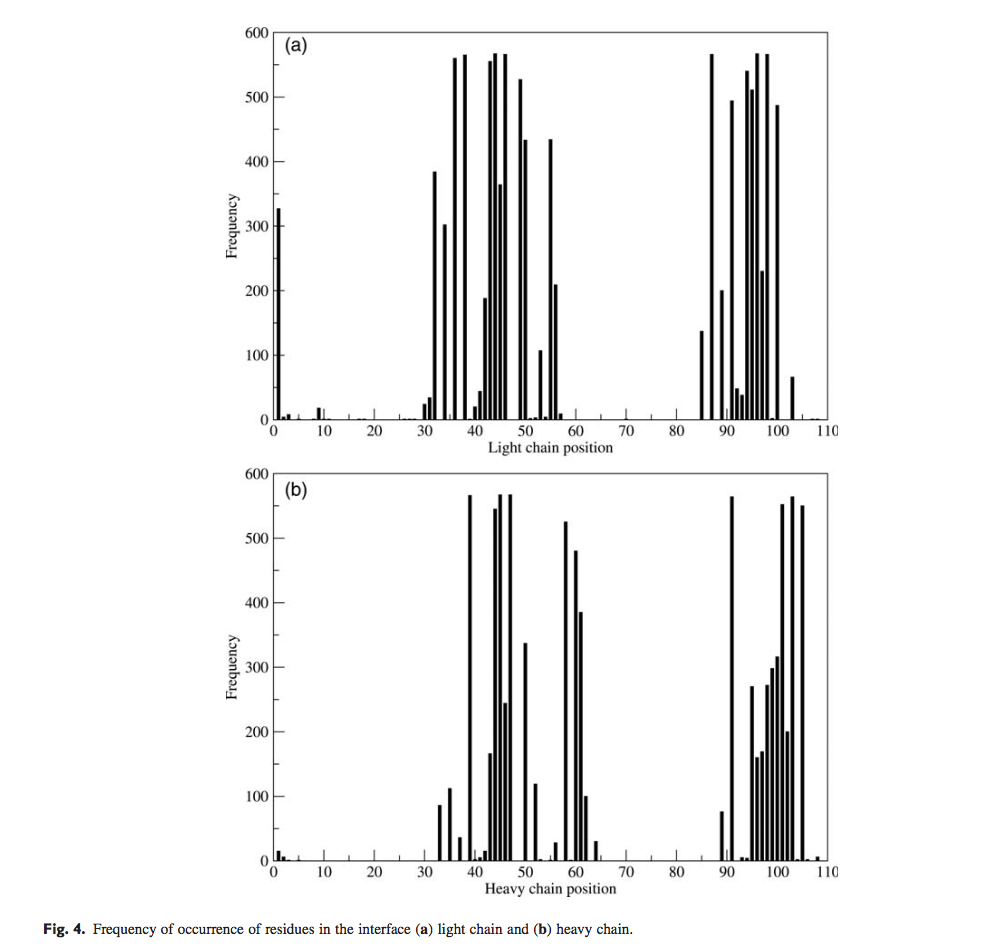
基于溶剂可及性的变化,总共124个Chothia编号的氨基酸位置(轻链中63个和重链中61个),至少在567个结构中的表面中出现一次。
如材料和方法中所述,需要“特征选择”过程来选择这124个潜在界面位置的残基以训练神经网络。 最初,基于对溶剂可及表面积的变化和界面中出现频率的分析,手动选择最可能影响填充角度的20个界面残留物(10个轻和10个重)(图4)。 由于VH / VL填充角度的可变性,任何给定结构中的界面残基将是在所有观察到的结构中识别的总集合的子集。 表I显示了基于以下的四种界面残留物的手动选择:(i)溶剂可及表面积( accessible surface area ,ASA)的最大变化,(ii)ASA的最高平均变化(highest average change in ASA),(iii)ASA中具有最高变化的最频繁发生的位置(most frequently occurring positions with highest change in ASA ) (iv)最常见的ASA平均变化最高的位置( most frequently occur- ring positions with highest average change)
表I还显示了基于手动选择界面位置的训练和验证神经网络的结果。 由于所有方法的5倍交叉验证的Pearson相关系数(r)都很低,因此没有一种手动选择界面残留的方法工作得特别好。 然而,从个体褶皱的检查中,观察到高达0.6的相关系数使我们确信数据确实具有有用的预测能力。 因此,设计了一种新策略以改进训练特征选择

不是基于界面中的可访问性和出现来选择用于预测打包角度的界面残差,而是决定使用GA来进行特征选择。GA旨在选择最多20个表面位置,这些位置在训练神经网络时是最佳的。
当仅考虑框架残基表明CDR残基对VH / VL包装仅具有小的影响时(数据未显示),总体性能更好。
因此,此处仅报告仅使用框架残基的结果。
最后的用于构建模型的残基为:
L38, L40, L41, L44, L46, L87, H33, H42, H45, H60, H62, H91
and H105
预测的得分见下图:
最好得分为0.833

2.6 背景介绍
Analysis and prediction of VH/VL packing in antibodies
抗体的可变性编码在可变片段(或Fv区)中,其分别由来自重链和轻链的两个蛋白结构域(VH和VL)组成。已经显示影响Fv区稳定性的VH / VL界面影响肽的结合动力学(Chatellier等,1996)。 VH / VL界面处的框架区由两个b片组成(Poljak等,1973),其结构在Fv,Fab和轻链二聚体上是保守的(Chothia等,1985; Novotny和Haber, 1985)。 Chothia等人详细分析了VH和VL结构域的包装(packing)。 (1985)。他们认识到VH / VL packing 涉及“three-layer packing”,主要是芳香族侧链参与界面。然而,该分析仅基于三种抗体结构,数据集太小而无法分析包装角度(packing angle)的变化。他们只是说角度是~ -50°,尽管他们没有说明这个值是如何计算的。
框架区中的残基对与抗原相互作用的贡献仍然知之甚少。 已经证明,相对远离抗体的抗原结合位点的残基的修饰可以对抗原的结合亲和力具有显着影响(Chatellier等,1996; Roguska等,1996; Adair等。 ,1999)。 例如,Adair等。 (1999)证明残基H23的修饰可显着影响抗体和抗原的结合。
早期关于抗体建模的研究忽略了VH / VL包装(packing)的变异(Martin等,1989; Martin等,1991; Whitelegg和Rees,2000),尽管最近的研究已经开始将其视为一个重要因素(Narayanan) et al。,2009; Sircar et al。,2009; Sivasubramanian et al。,2009)。 然而,已经完成的工作还没有包括对包装角度分布的全面分析,并且相互作用的预测使用了计算密集型能量计算
在这里,我们提出了VH / VL包装角分布的分析和使用机器学习预测界面角度的方法。 经过训练的机器学习方法能够提供非常快速的包装角度预测。 在对可变区轻链和重链建模之前知道填充角度可以帮助选择模型可以基于的更合适的模板结构
人源化过程涉及将鼠CDR移植到人框架区域上(Jones等,1986)。 可能需要进一步修饰框架残基以恢复小鼠抗体的结合亲和力(Riechmann等,1988)。 Adair专利(Adair等,1999)包括VH / VL界面残基作为残留类别之一,可能需要匹配其鼠类对应物以保持互补位的地形。 然而,关于哪些残留物可能具有最大影响的指导是有限的。
因此,这项工作有两个主要应用:(i)在抗体建模中,以预测正确的包装角度;和(ii)识别在确定包装角度中重要的关键界面残基,以便改善抗体人源化
三、待理解的地方
- GA算法的实现
- angle这条线的确定
四、讨论
- 这个工具预测出来的夹角,与ABangle的一比较,就凉凉了。。
参考资料
- https://github.com/ACRMGroup/papa
- 《Analysis and prediction of VH/VL packing in antibodies》
