【4.3.2】基于序列预测线性BCE--Bepipred-1.0

预测网址： http://tools.iedb.org/bcell/

BepiPred predicts the location of linear B-cell epitopes using a combination of a hidden Markov model and a propensity scale method. The residues with scores above the threshold (default value is 0.35) are predicted to be part of an epitope and colored in yellow on the graph (where Y-axes depicts residue scores and X-axes residue positions in the sequence) and marked with “E” in the output table. The values of the scores are not affected by the selected threshold. The table below shows the relationship between selected thresholds and the sensitivity/specificity of the prediction method, calculated on basis of the epitope/non-epitope predictions. The table is based on a large benchmark calculation containing close to 85 B cell epitopes.

Threshold	Sensitivity	Specificity
-0.20	0.75	0.50
0.20	0.56	0.68
0.35	0.49	0.75
0.90	0.25	0.91
1.30	0.13	0.96

• 背景： B细胞表位是免疫系统抗体识别的分子位点。 B细胞表位的知识可用于疫苗设计和诊断测试。因此，有兴趣开发用于预测B细胞表位的改进方法。在本文中，我们描述了一种预测线性B细胞表位的改进方法。

• 结果： 为此，构建了线性B细胞表位注释蛋白的三个数据集。从文献中收集了一个数据集，从AntiJen数据库中提取了另一个数据集，并从Los Alamos HIV数据库中收集了HIV蛋白质表位的数据集。通过在既未对其进行训练也未对其进行优化的数据集上进行测试，对方法进行了公正的验证。我们通过构建ROC曲线以非参数的方式测量了性能。

• 结论： 预测线性B细胞表位的最佳单一方法是隐马尔可夫模型。将隐马尔可夫模型与最佳倾向标度方法之一相结合，我们获得了BepiPred方法。在验证数据集上进行测试时，该方法的性能明显优于其他任何测试方法。服务器和数据集可在 http://www.cbs.dtu.dk/services/BepiPred 上公开获得。

一、背景

疫苗主要由灭活或减毒的完整病原体组成。然而，出于安全原因，可能希望使用能够产生针对特定病原体的免疫反应的肽疫苗[1]。这样的疫苗可以包含代表来自病原体蛋白质的线性B细胞表位的肽。休斯等[2]使用线性B细胞表位在小鼠中诱导针对铜绿假单胞菌的保护性免疫。通过免疫动物，含有线性B细胞表位的合成肽也可用于产生针对特定蛋白质的抗体，例如，可用于筛选测定或作为诊断工具[3]。

B细胞表位是抗体（由B细胞制造）结合的蛋白质或其他分子的一部分。大多数蛋白质表位由多肽链的不同部分组成，这些部分通过蛋白质折叠而在空间上接近。这些表位被称为不连续的，但对于约10％的表位，相应的抗体可与表位的线性肽片段发生交叉反应[4]。这些表位被表示为线性或连续的，并且主要由多肽链的单段组成。

即使线性B细胞表位在体液免疫反应的详细理解中具有有限的相关性，但在病原生物中寻找抗原决定簇时，这种线性肽段的鉴定通常仍是第一步。在基因组规模上，传统的实验性肽扫描方法显然是不可行的。预测方法是非常经济有效的方法，因此预测线性B细胞表位的可靠方法将是指导病原生物中全基因组搜索B细胞抗原的第一步。

预测线性B细胞表位的经典方法是使用倾向标度法（propensity scale methods）。这些方法根据对每种氨基酸的理化特性的研究，为它们分配了一个倾向值。预测值序列的波动可通过应用移动平均值窗口来减少。这种预测程序最初是由Hopp和Woods [5]开发的。

Pellequer等[4]比较了使用14种表位注释蛋白的数据集的几种倾向量表。他们发现应用了Parker等人的量表 [6]（亲水性），Chou和Fasman [7]和Levitt [8]（二级结构）以及Emini等人[9]（可访问性）比其他测试量表提供了更好的结果。

Alix [10]开发了一个名为PEOPLE的程序，该程序使用倾向性标度方法的组合预测线性B细胞表位的位置。 Odorico [11]开发了一个程序BEPITOPE，用于使用倾向标度方法预测线性B细胞表位的位置。

最近，Blythe和Flower [12]研究了许多倾向量表方法的性能，发现即使最好的方法也只能比随机模型更好地预测。他们使用来自AntiJen网页 http://www.jenner.ac.uk/AntiJen [50]的50个表位定位蛋白的数据集进行了深入研究。

在这项研究中，我们开发了一种预测线性B细胞表位的新方法BepiPred，该方法的性能远胜于随机预测，也远胜于许多测试的倾向量表。

尽管本方法相对于用于预测线性B细胞表位的早期方法有显着改进，但它仍具有很大的局限性。在这样的系统普遍用于提供B细胞表位的可靠预测之前，需要进一步提高预测能力。

二、结果

2.1 倾向量表方法的预测

我们首先在Pellequer数据集上测试了许多倾向标度方法[14]。 对于每个比例尺和窗口大小，计算ROC曲线及其下的面积A roc值，作为预测准确性的度量。 从预测中提取了1000个引导程序样本，以估计A roc值的标准误差。 Levitt [8]发现最佳比例（窗口大小为11，Aroc = 0.658±0.013）。 该方法将称为Levitt。 第二好的量表是Parker等人的量表。[6]（窗口大小9，Aroc = 0.654±0.013），表示为Parker。 经过测试的其他量表的性能不如Parker等人[6]和Levitt [8]的量表。

通过执行1000次置换实验，我们估算了方法执行类似于随机模型的假设的P值，替代假设是该方法的性能优于随机模型。 Parker and Levitt 的所得P值均低于0.1％。

2.2 隐马尔可夫模型的预测

进行了实验，其中使用隐马尔可夫模型（HMM）来预测线性B细胞表位的位置。 这些方法是从AntiJen数据集中提取的正窗口构建的。 在Pellequer数据集上测试了HMM，以找到最佳参数。 测试了提取的肽窗口的大小不同，用于估计氨基酸频率的伪计数校正的权重不同以及平滑窗口的大小不同。 对于最佳方法，发现提取的窗口大小为5，平滑窗口的大小为9，伪计数校正为10^7。该方法在Pellequer数据集上的性能为A roc = 0.663± 0.012。 具有这些参数的此方法将表示为HMM。

2.3 组合方式

为了做出更准确的预测，将隐马尔可夫模型（HMM）与两种最佳倾向量表方法之一（Parker和Levitt）相结合。 组合作为归一化预测值的加权和完成。 两种方法的权重之和保持等于，并测试了不同的权重对。 Pellequer数据集用于优化参数值。 选择了具有最高A roc值的组合方法进行进一步比较，并在表1中进行了显示。具有最高A roc值的组合方法表示为BepiPred，它是预测线性B细胞表位的候选方法。 它是HMM和Parker的组合。

2.4 验证方法

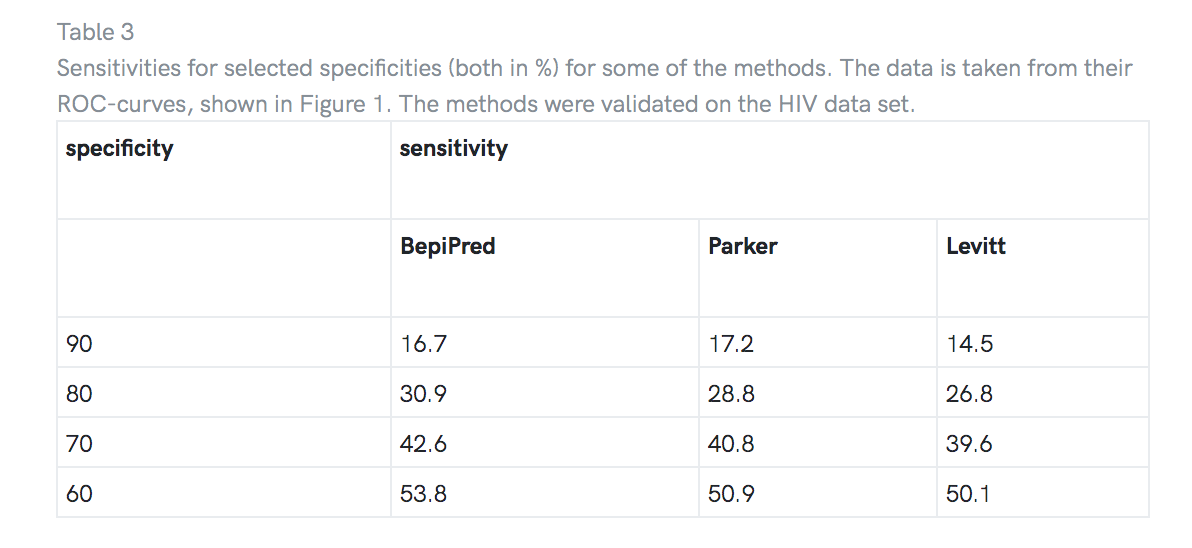
为了对方法进行公正的验证，对独立的数据集HIV数据集进行了测试。 结果显示在表2中。再次将BepiPred视为最佳方法。 所选方法的ROC曲线如图1所示，所选值在表3中给出。

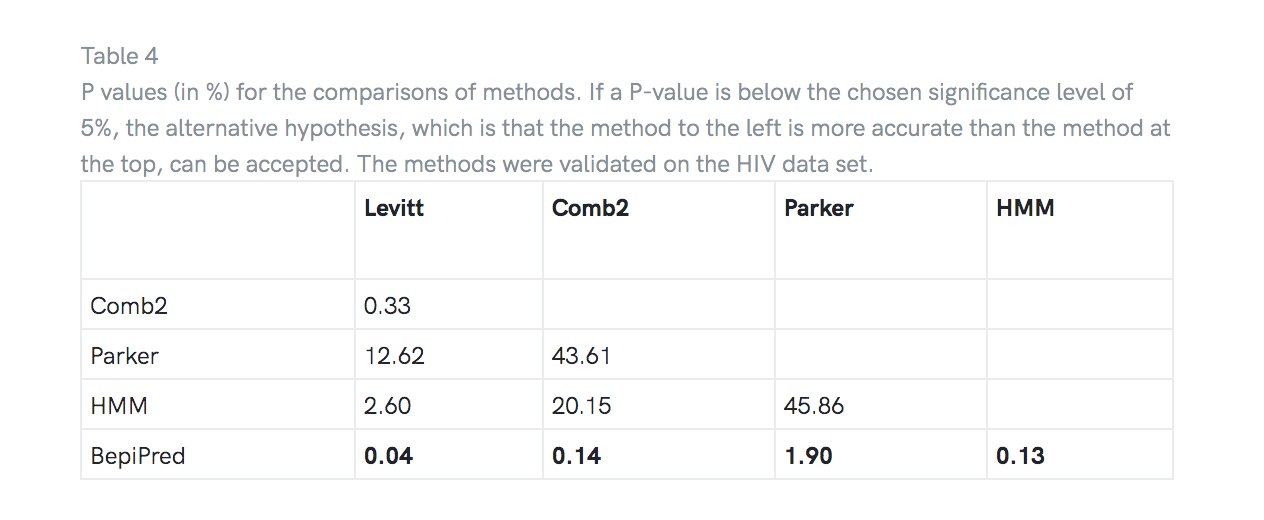
对HIV数据集进行了预测的配对t检验，以确定一种方法的预测准确性是否明显高于另一种方法。 表4显示，发现BepiPred显着优于所有其他测试方法，而HMM却没有显着优于Parker。

三、讨论

我们使用隐马尔可夫模型构建了线性B细胞表位的预测方法。隐藏的马尔可夫模型以前从未用于此特定目的。

我们的方法灵敏度很低。提高灵敏度的一种方法是降低应用的阈值，但这也会导致较低的特异性。 Pellequer等人[14]结果表明，通过组合预测曲线可以减少过度预测，并且可以使用类似方法进一步改善B细胞表位的预测方法。

Pellequer等[4]使用本研究中的数据集之一：Pellequer数据集，比较了几个倾向量表。他们进行了一项研究，对数据集应用了一些倾向标度方法，并使用了0.7 s的固定阈值，其中s是预测值的标准偏差。此阈值将预测分类为肯定或否定。他们发现使用不同量表的预测要好于随机数，符合本研究的结果。他们在由9个序列组成的数据集上比较了这些量表，发现Parker等人的量表[6]，Chou和Fasman [7]，Levitt [8]和Emini等人[9]给出了比其他测试量表更好的结果。

在本研究中，我们发现对于类似的数据集，效果最好的量表由Levitt [8]和Parker等人构建[6]。这与Pellequer等人的发现非常吻合。 [4]。

Blythe和Flower [12]发现，即使是最佳的倾向量表方法，其效果也仅比随机模型好一点。他们使用了来自AntiJen主页 http://www.jenner.ac.uk/AntiJen[13] 的50个抗原决定簇定位蛋白的数据集，并对数据应用了许多倾向量表方法。

我们的置换测试表明，Parker等人的量表 [6]和Levitt [8]拥有最佳的窗口大小，其性能明显优于随机模型。

我们已经测试了几种倾向量表方法，并优化了它们的参数，以便确定最佳方法。对于Pellequer数据集，发现最佳方法是[8]的标度，窗口大小为11。第二个最佳倾向标度方法是Parker等人的标度。 [6]的窗口大小为7-11。作者打算将此比例尺用于7的窗口大小，这与我们的发现非常吻合。

四、结论

我们提出了一种预测线性B细胞抗原决定簇BepiPred的新颖方法。这是一种组合方法，是通过将隐藏的马尔可夫模型的预测与倾向性比例（由Parker等人）组合而成。 [6]。为了优化隐马尔可夫模型和倾向标度法，我们测试了不同的参数。

我们已经使用非参数ROC曲线对方法进行了测试，并使用单独的数据集进行了无偏验证。我们发现BepiPred在测试数据集上具有最高的预测准确度，并且显示出比在验证数据集上测试的所有其他方法明显更好的性能。将BepiPred与验证数据集上的最佳倾向量表方法进行比较，特异性为BepiPred（Parker等人的量表）的灵敏度为80％。 [6]和Levitt[8]分别是30.9％，28.8％和26.8％。

未来的工作可能包括使用其他来源的数据，例如免疫表位数据库和分析资源IEDB [15]或蛋白质中结构推断的抗原表位的Epitome数据库 http://www.rostlab.org/services/epitome 。

五、数据集

在这些研究中使用了三个带有线性B细胞表位注释的蛋白质数据集。通过测量完整蛋白和肽片段之间的交叉反应性来构建所有数据集[16]。

5.1 Pellequer数据集

数据集用于测试和方法的优化。由于该数据集无法以电子形式获得，因此由Lund等人重新创建[17]。表位注释来自Pellequer等[14]及其参考。蝎神经毒素的序列是一个例外，该数据取自[18]。该数据集表示为Pellequer数据集，包含14个蛋白质序列和83个表位。表位密度是0.34。

5.3 AntiJen数据集

第二个数据集用于训练和构建隐马尔可夫模型。该数据集是从AntiJen数据库（以前是JenPep [13] http://www.jenner.ac.uk/AntiJen ）中提取的。该数据集称为AntiJen数据集，由127个蛋白序列组成，表位密度为0.08。此数据集的蛋白质未完全注释，并且非表位延伸的注释未知。

5.4 艾滋病毒数据集

制作了一个单独的数据集，可对方法进行无偏验证。它由从洛斯阿拉莫斯国家实验室（Los Alamos National Laboratory）[19] http://www.hiv.lanl.gov 的HIV分子免疫学数据库中获得的HIV蛋白质中发现的表位组成。该数据集中的表位在一定程度上重叠。因此，将用于确定最小表位的更准确边界的方法应用于表位。如果包含较小的抗原决定簇作为较大抗原决定簇的一部分，则将从数据集中丢弃较大抗原决定簇。其中两个序列没有指定的表位，因此从数据集中被丢弃。 HIV数据集由10个蛋白质序列组成，表位密度为0.38。

六、方法

6.1 倾向量表方法 Propensity scale methods

倾向量表方法将倾向值分配给查询蛋白序列的每个氨基酸。通过应用运行中的均值窗口可以减少波动。在N端和C端，我们使用不对称窗口以避免丢弃预测示例。本研究中使用的标度基于抗原性[20]，亲水性[6]，反向疏水性[21，22]，可及性[9]和二级结构[7，8]。

6.2 隐马尔可夫模型

令i ＝（i1，i2，…，i w）表示从蛋白质序列中提取的氨基酸序列。令j表示此窗口中的位置，j = 1 … w。基于i，隐藏的马尔可夫模型预测窗口的中心位置是否被注释为表位的一部分。在N端和C端，提取的窗口的一部分超出了终端。对于这些残基，使用字符“ X”，当将隐马尔可夫模型用于预测时，该字符不计数。窗口的预测得分为

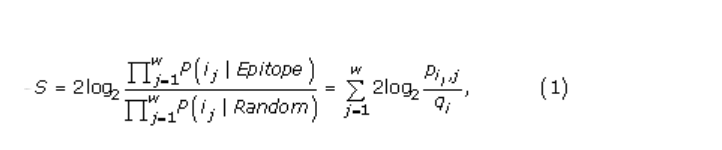
与窗口偶然出现的残基（随机模型）相反，它是窗口中心位置的残基的对数几率正成为表位的一部分（表位模型）。

为了构造随机模型，使用Swiss-Prot数据库[23]的背景频率q i。对于表位模型，p i，j是根据模型在位置j处具有氨基酸i的有效氨基酸概率。

为了计算p i，j的值，从训练数据集中提取所有窗口，这些窗口的中心位置被注释为表位的一部分。同样，如果提取的窗口超过N或C端子，则使用字符“ X”，该字符在计算参数时不计数。

这些提取的肽窗口形成了宽度为w的对齐肽矩阵。从该比对中，将p i，j计算为第[j]列中第i列氨基酸i的伪计数校正概率，如[24]中所估计。为了进行伪计数校正，计算伪计数频率g i，j。它们由

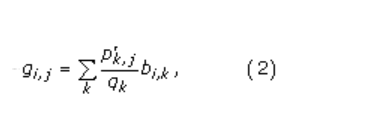
其中，p(k，j)是比对[25]的第j列中观察到的氨基酸k的频率。 变量b( i，k)是Blosum 62替换矩阵频率，例如。 i的频率与k对齐[26]。

举一个使用（2）的例子，设窗口大小w =1。然后，该模型仅覆盖残基，这些残基被注释为线性B细胞表位的一部分。 如果观察到的肽由以下单个氨基酸序列L和V组成，其频率为p(L，1) ＝ 0.5和p(V，1) ＝ 0.5，则伪计数频率为例如。 我是由

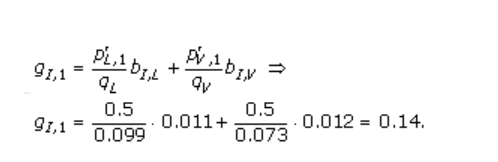
有效氨基酸频率计算为观察频率和伪计数频率的加权平均值，

这里，α是比对-1中的有效序列数，β是伪计数校正[25]，也称为低计数权重。 为了完成计算示例，让β很大，因为它在这项工作中。 那么p(I，1)≈g(I，1 )= 0.14。

注意，在整个工作中，我们将使用术语“隐马尔可夫模型”来指代使用（1）生成的权重矩阵。 无间隙马尔可夫模型的参数是使用Nielsen等人编写的所谓的Gibbs采样器计算的。 [24]。

应用（1）的结果是查询序列中每个残基的预测得分。 为了减少波动，将平滑窗口应用于每个位置。 为了保留预测示例，它在N端和C端不对称。

6.3 ROC曲线

将预测方法应用于数据集的结果是一组预测示例x =（x 1，x 2，…，x N）。令n表示残基数。每个x n由一个目标值和一个预测值组成。如果将残基标注为表位的一部分，则目标值为1，否则为零。如果在N端和C端使用非对称平滑窗口，则变量N等于数据集中的残基数。

根据可变阈值，将预测示例分为正或负，并且根据目标值，预测可以为真或假。预测可以是真阳性（TP），真阴性（TN），假阳性（FP）或假阴性（FN）。

预测精度(accuracy)是通过构建接收机工作特性ROC曲线来衡量的[27]。对于阈值的每个值，计算真实的正比例TP /（TP + FN）和错误的正比例FP /（FP + TN）。通过将阈值所有值的假阳性比例与真阳性比例作图来构造ROC曲线。因此，这是一种非参数度量。

灵敏度(sensitivity)等于真实阳性比例，而由TN /（FP + TN）给出的特异性等于1 –假阳性比例。这样，ROC曲线显示了所有可能阈值的灵敏度和特异性之间的权衡。好的方法的假阳性率低，假阳性率高。这样的模型具有高灵敏度和高特异性。该方法的性能以曲线下的面积A roc值表示。对于随机预测，对于每个阈值，真实正比例等于错误正比例。那么A roc = 0.5。对于一个完美的方法，A roc = 1。

6.4 Bootstrapping

6.5 Paired t-tests

6.6 Permutation tests

批注

1. HMM的推导过程还不是太明白，留坑回头看研究。

参考资料

• Reference: Jens Erik Pontoppidan Larsen, Ole Lund and Morten Nielsen. Improved method for predicting linear B-cell epitopes. Immunome Res. 2006; 网址： https://www.neueve.com/content/2/1/2