【1】概率推理

虽然还不能完全理解下面两幅图的含义。。

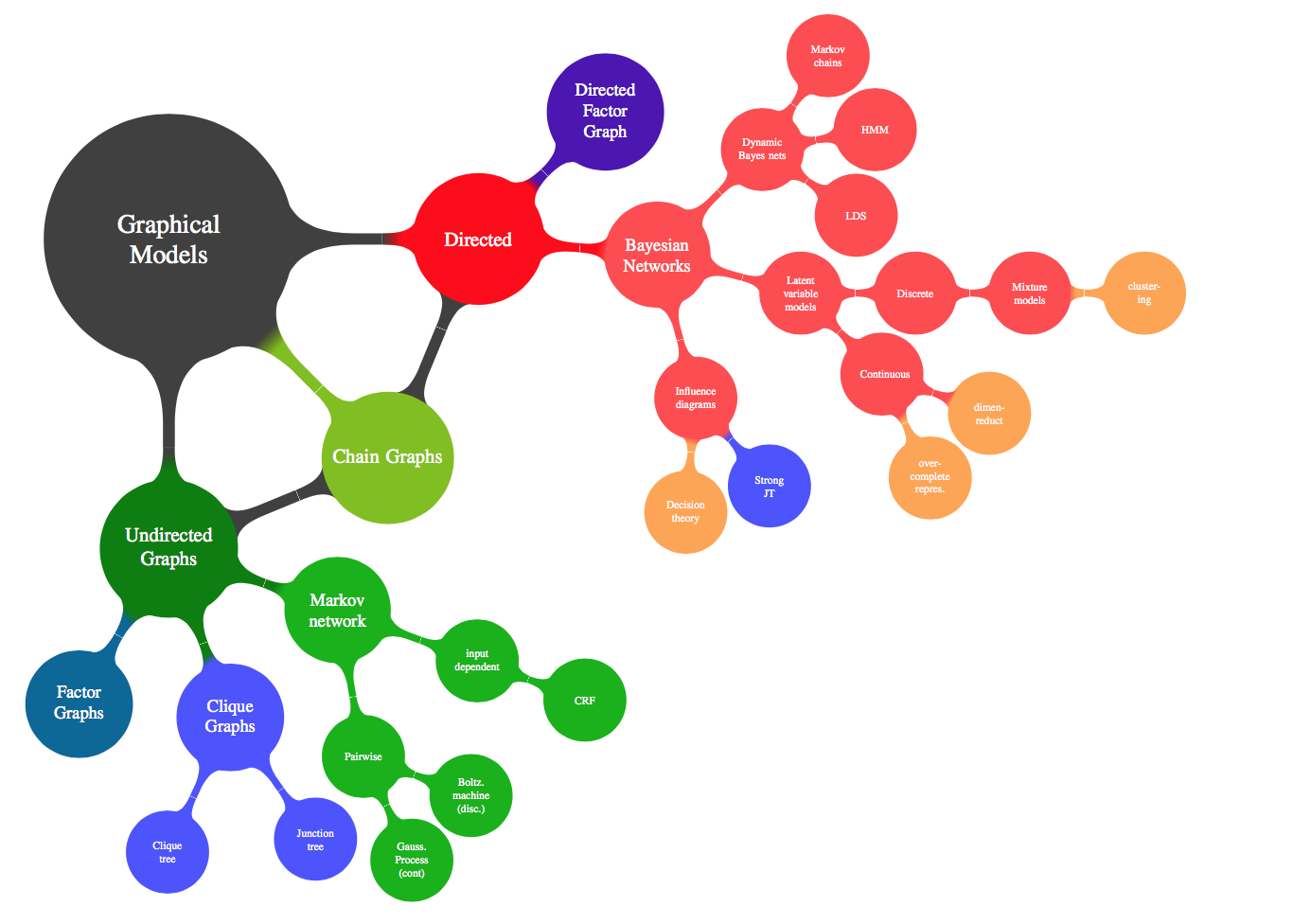
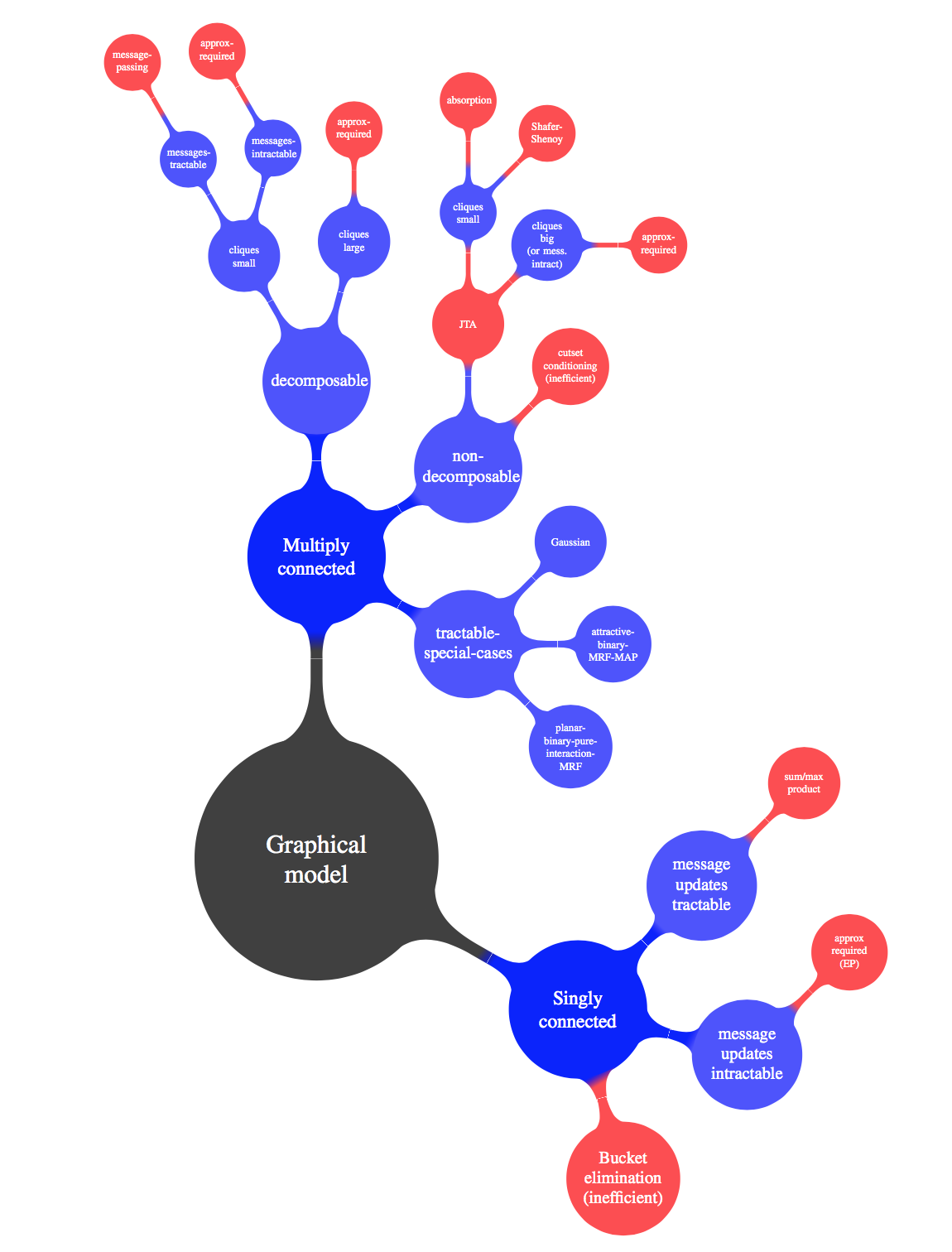
一. 概率基本概念

变量，状态，代表的符号

变量可以用大写字母 X 或者用小写字母 x 表示，一个变量的集合可以通过一个书写符号(calligraphic symbol)表示，例如： V = {a, B, c}

变量x的域记作dom(x)，表示x可以的取值范围。（一般这个x都sans-serif字体）。例如，对于投硬币的事件c,dom(c) = {heads,tails}，其中p(c = heads)代表变量c为heads的时候的概率，一般简写为p(heads)。p(state) 就是代表概率，不用专门把变量的符号写出来。 ∑_xf(x)，代表x的所有取值下的概率和，例如：∑_x∈dom(x)f(x=s)。

例如，投币事件， p(The coin is tails) 可以解释为 p(The coin is tails = true)。我们可以记作p(x = tr)，代表发生x为真的时候的概率.或者 p(x = fa)代表x为假（false）状态下的概率

定义1.1：离散变量的概率规则（Rules of Probability for Discrete Variables）

变量x在状态x时候的概率 p(x = x)取值在0，1之间。p(x = x)=1代表包含了x的所有取值。相反的，p(x = x)=0代表取值不在域里面。

$$\sum_{x∈dom(x)}p(x = x) = 1$$

这被称作normalisation condition。我们可以简写为∑_xp(x) =1

两个变量的并集可以写作

p(x = a or y = b) = p(x = a) + p(y = b) − p(x = a and y = b)

或者，简写为：

p(x or y) = p(x) + p(y) − p(x and y )

我们可以用p(x, y)代替 p(x and y)。同时 p(y, x) = p(x, y) 和 p(x or y) = p(y or x)。

定义1.2 设置符号（Set notation）

p(x or y) ≡ p(x ∪ y), p(x, y) ≡ p(x ∩ y)

定义1.3 边界值（Marginals）

$$ p(x) = \sum \limits_{y}p(x,y) $$

p(x)是联合概率分布p(x,y)的边际。求联合概率分布的边际的过程叫做边缘化（marginalisation）。

$$ p(x_{1},x_{i-1},x_{i+1},...,x_{n}) = \sum \limits_{x_{i}}p(x1,...,xn) $$

定义1.4 条件概率/贝叶斯 (Conditional Probability / Bayes’ Rule)

在y发生的情况下x发生的概率

参考资料：

http://web4.cs.ucl.ac.uk/staff/D.Barber/pmwiki/pmwiki.php?n=Main.Software

http://www.cs.ucl.ac.uk/staff/D.Barber/brml

Bayesian Reasoning and Machine Learning