【3】无监督学习--3--聚类--基于距离--kmeans
一、简介
k-means algorithm算法是一种得到最广泛使用的基于划分的聚类算法,把n个对象分为k个簇,以使簇内具有较高的相似度。相似度的计算根据一个簇中对象的平均值来进行。它与处理混合正态分布的最大期望算法很相似,因为他们都试图找到数据中自然聚类的中心。
算法首先随机地选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇,然后重新计算每个簇的平均值。这个过程不断重复,直到准则函数收敛。
$$V = \sum_{i=1}^{k} \sum_{x_j \in S_i} (x_j - \mu_i)^2$$
它假设对象属性来自于空间向量,并且目标是使各个群组内部的均方误差总和最小。假设有k个群组Si, i=1,2,…,k。μi是群组Si内所有元素xj的重心,或叫中心点。
术语“k-means”最早是由James MacQueen在1967年提出的,这一观点可以追溯到1957年 Hugo Steinhaus所提出的想法。1957年,斯图亚特·劳埃德最先提出这一标准算法,当初是作为一门应用于脉码调制的技术,直到1982年,这一算法才在贝尔实验室被正式提出。1965年, E.W.Forgy发表了一个本质上是相同的方法,1975年和1979年,Hartigan和Wong分别提出了一个更高效的版本。
二、算法
k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。
其处理过程如下:
- 随机选择k个点作为初始的聚类中心;
- 对于剩下的点,根据其与聚类中心的距离,将其归入最近的簇
- 对每个簇,计算所有点的均值作为新的聚类中心
- 重复2、3直到聚类中心不再发生改变
算法描述
输入:簇的数目k;包含n个对象的数据集D。
输出:k个簇的集合。
方法:
从D中任意选择k个对象作为初始簇中心;
repeat;
根据簇中对象的均值,将每个对象指派到最相似的簇;
更新簇均值,即计算每个簇中对象的均值;
计算准则函数;
until准则函数不再发生变化。
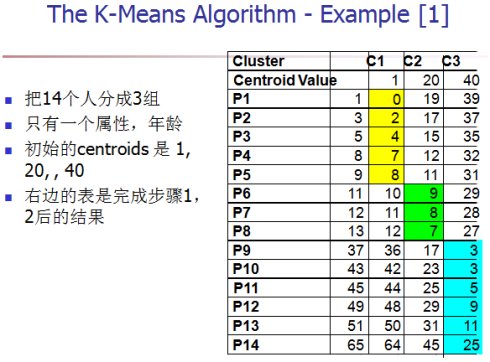
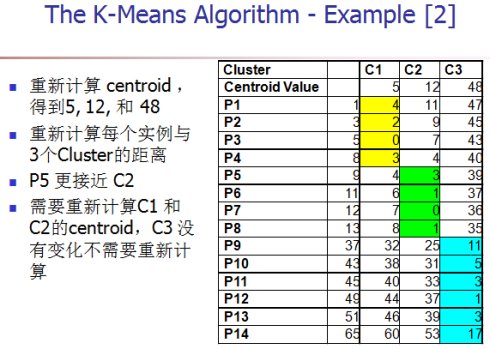
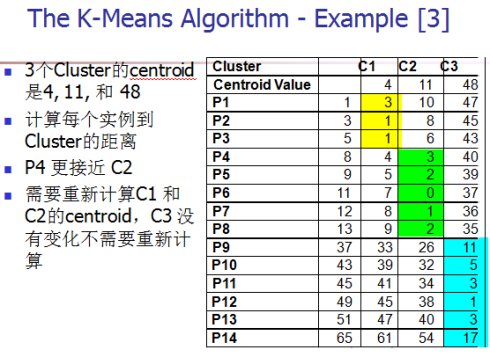
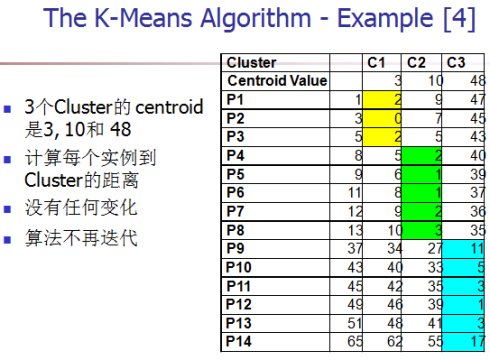
算法的性能分析
1)优点
(1)k-平均算法是解决聚类问题的一种经典算法,算法简单、快速。
(2)对处理大数据集,该算法是相对可伸缩的和高效率的,因为它的复杂度大约是O(nkt),其中n是所有对象的数目,k是簇的数目,t是迭代的次数。通常k«n。这个算法经常以局部最优结束。
(3)算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的,而簇与簇之间区别明显时,它的聚类效果很好。
2)缺点
(1)k-平均方法只有在簇的平均值被定义的情况下才能使用,不适用于某些应用,如涉及有分类属性的数据不适用。
(2)要求用户必须事先给出要生成的簇的数目k。
(3)对初值敏感,对于不同的初始值,可能会导致不同的聚类结果。
(4)不适合于发现非凸面形状的簇,或者大小差别很大的簇。
(5)对于"噪声"和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
三、K-means的应用
官网例子;
from sklearn.externals import joblib
>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 4], [4, 0]])
#调用kmeans类
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
#9个中心
print clf.cluster_centers_
#每个样本所属的簇
>>> kmeans.labels_
array([0, 0, 0, 1, 1, 1], dtype=int32)
#用来评估簇的个数是否合适,距离越小说明簇分的越好,选取临界点的簇个数
print clf.inertia_
#进行预测
>>> kmeans.predict([[0, 0], [4, 4]])
array([0, 1], dtype=int32)
>>> kmeans.cluster_centers_
array([[ 1., 2.],
[ 4., 2.]])
#保存模型
joblib.dump(clf , 'c:/km.pkl')
#载入保存的模型
clf = joblib.load('c:/km.pkl')
#用来评估簇的个数是否合适,距离越小说明簇分的越好,选取临界点的簇个数
for i in range(5,30,1):
clf = KMeans(n_clusters=i)
s = clf.fit(feature)
print i , clf.inertia_
调用KMeans方法所需参数:
-
n_clusters:用于指定聚类中心的个数
-
init:初始聚类中心的初始化方法;k-means++’ 会由程序自动寻找合适的n_clusters;
类型:可以是function 可以是array(random or ndarray) 默认值:采用k-means++(一种生成初始质心的算法)
kmeans++:种子点选取的第二种方法。 kmedoids(PAM,Partitioning Around Medoids)
能够解决kmeans对噪声敏感的问题。kmeans寻找种子点的时候计算该类中所有样本的平均值,如果该类中具有较为明显的离群点,会造成种子点与期望偏差过大。例如,A(1,1),B(2,2),C(3,3),D(1000,1000),显然D点会拉动种子点向其偏移。这样,在下一轮迭代时,将大量不该属于该类的样本点错误的划入该类。
为了解决这个问题,kmedoids方法采取新的种子点选取方式,1)只从样本点中选;2)选取标准能够提高聚类效果,例如上述的最小化J函数,或者自定义其他的代价函数。但是,kmedoids方法提高了聚类的复杂度。
init : {'k-means++', 'random' or an ndarray} Method for initialization, defaults to 'k-means++': 'k-means++' : selects initial cluster centers for k-mean clustering in a smart way to speed up convergence. See section Notes in k_init for more details. -
max_iter:最大的迭代次数,这里设置最大迭代次数为300;
-
一般调用时只用给出n_clusters即可,init
-
n_init设为10意味着进行10次随机初始化,选择效果最好的一种来作为模型; 类型:整数型(int)
默认值:10
目的:每一次算法运行时开始的centroid seeds是随机生成的, 这样得到的结果也可能有好有坏. 所以要运行算法n_init次, 取其中最好的。
n_init : int, default: 10 Number of time the k-means algorithm will be run with different centroid seeds. The final results will be the best output of n_init consecutive runs in terms of inertia.
-
tol:float形,默认值= 1e-4,与inertia结合来确定收敛条件; 容忍的最小误差,当误差小于tol就会退出迭代(算法中会依赖数据本身)
-
n_jobs:指定计算所用的进程数;
-
verbose 参数设定打印求解过程的程度,值越大,细节打印越多;
-
copy_x:布尔型,默认值=True。当我们precomputing distances时,将数据中心化会得到更准确的结果。如果把此参数值设为True,则原始数据不会被改变。如果是False,则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算,所以数据返回后,原始数据和计算前可能会有细小差别。
-
precompute_distances: 这个参数会在空间和时间之间做权衡,如果是True 会把整个距离矩阵都放到内存中,auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False时核心实现的方法是利用Cpython 来实现的
类型:布尔型(auto,True,False) 默认值:“auto”
-
random_state: 随机生成器的种子 ,和初始化中心有关 ;类型:整型或numpy(RandomState, optional);默认值:None
其它参数:
- data:加载的数据
- label:聚类后各数据所属的标签
- axis: 按行求和
- fit_predict():计算簇中心以及为簇分配序号
其他属性
- cluster_centers_:向量,[n_clusters, n_features] Coordinates of cluster centers (每个簇中心的坐标??);
- Labels_:每个样本对应的簇类别标签
- inertia_:float,每个点到其簇的质心的距离之和。
对于非监督机器学习,输入的数据是样本的特征,clf.fit(X)就可以把数据输入到分类器里。;用分类器对未知数据进行分类,需要使用的是分类器的predict方法。
案例一
数据介绍:
K-means的应用
现有1999年全国31个省份城镇居民家庭平均每人全年消费性支出的八个主 要变量数据,这八个变量分别是:食品、衣着、家庭设备用品及服务、医疗 保健、交通和通讯、娱乐教育文化服务、居住以及杂项商品和服务。利用已 有数据,对31个省份进行聚类。
##实验目的:
通过聚类,了解1999年各个省份的消费水平在国内的情况。
使用算法: K-means聚类算法 • 实现过程:
1.建立工程,导入sklearn相关包
import numpy as np
from sklearn.cluster import KMeans
关于一些相关包的介绍:
NumPy是Python语言的一个扩充程序库。支持高级大量的维度数组与矩阵运算,此外也针对数组 运算提供大量的数学函数库。 使用sklearn.cluster.KMeans可以调用K-means算法进行聚类
#coding:UTF-8
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import numpy as np
from sklearn.cluster import KMeans
def loadData(filePath):
fr = open(filePath,'r+')
lines = fr.readlines()
retData = []
retCityName = []
for line in lines:
items = line.strip().split(",")
retCityName.append(items[0])
retData.append([float(items[i]) for i in range(1,len(items))])
return retData,retCityName
if __name__ == '__main__':
data,cityName = loadData('课程数据/聚类/31省市居民家庭消费水平-city.txt') #数据集的位置 https://pan.baidu.com/s/1kV0uFrh
km = KMeans(n_clusters=4)
label = km.fit_predict(data)
expenses = np.sum(km.cluster_centers_,axis=1)
#print(expenses)
CityCluster = [[],[],[],[]]
for i in range(len(cityName)):
CityCluster[label[i]].append(cityName[i])
for i in range(len(CityCluster)):
print("Expenses:%.2f" % expenses[i])
print(CityCluster[i])
四、 拓展&&改进
计算两条数据相似性时,Sklearn 的K-Means默认用的是欧式距离。虽然还有余弦相 似度,马氏距离等多种方法,但没有设定计算距离方法的参数。
如果想要自定义计算距离的方式时,可以 更改此处源码。 def euclidean_distances(): 建 议 使 用 scipy.spatial.distance.cdist 方 法 源码地址: https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/metrics/pairwise.py
使用形式:scipy.spatial.distance.cdist(A, B, metric=‘cosine’)
参考资料:
- http://scikit-learn.org/stable/modules/clustering.html
- http://cwiki.apachecn.org/pages/viewpage.action?pageId=10814188
- 北京理工大学 礼欣 www.python123.org
- 维基百科:http://zh.wikipedia.org/wiki/K平均算法
- 水逝流年博客: http://blog.csdn.net/xia7139/article/details/9046687
- https://blog.csdn.net/EleanorWiser/article/details/70226704
- https://www.cnblogs.com/wuchuanying/p/6218486.html
