【4.3.2.9】量化预测结果--分类变量--MCC、RI
更平衡的评估标准包括:马修斯相关系数(Matthews correlation coefficient)和 ROC曲线。
马修斯相关性系数定义为
Matthews的原文中是这样描述这个系数的:
A correlation of:
C = 1 indicates perfect agreement,
C = 0 is expected for a prediction no better than random, and
C = -1 indicates total disagreement between prediction and observation
也就是说系数为1的时候,分类器是完美的,0的时候分类器和随机分类器没差,-1的时候分类器是最差的,所有预测结果和实际相反。那这样的系数是如何解决imbalance data问题呢?我们紧接着看他的数学形式:
$$ MCC = \frac{TP * TN - FP * FN}{ \sqrt{(TP +FP)(TP +FN)(TN + FP)(TN +FN) }}$$
需要注意的是,分母中任意一对括号相加之和如果为0,那么整个MCC的值就为0。我们再回归我们的老问题,对于TP=98,TN=0,FN=0,FP=2,由于TN,FN同时为0,那么MCC则为0,说明我们简单粗暴的方式和随机分类器没有异同。 MCC本质上是一个观察值和预测值之间的相关系数,维基百科上是这样评价MCC的:
While there is no perfect way of describing the confusion matrix of true and false positives and negatives by a single number, the Matthews correlation coefficient is generally regarded as being one of the best such measures
至此,我们解决了Accuracy Paradox问题,那么是不是说明我们可以只用MCC作为唯一标准呢,聪明的读者应该学会说不是了吧,Precsion和Recall可是很好地强调质和量的关系,并且能够通过F Measure体现出来,在很多情况下,用Accuracy作为指标也是一个不错的简单选择。
三、purity评价法:
purity方法是极为简单的一种聚类评价方法,只需计算正确聚类的文档数占总文档数的比例:
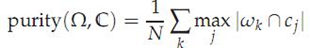
其中Ω = {ω1,ω2, . . . ,ωK}是聚类的集合ωK表示第k个聚类的集合。C = {c1, c2, . . . , cJ}是文档集合,cJ表示第J个文档。N表示文档总数。
如上图的purity = ( 3+ 4 + 5) / 17 = 0.71
其中第一类正确的有5个,第二个4个,第三个3个,总文档数17。
purity方法的优势是方便计算,值在0~1之间,完全错误的聚类方法值为0,完全正确的方法值为1。同时,purity方法的缺点也很明显它无法对退化的聚类方法给出正确的评价,设想如果聚类算法把每篇文档单独聚成一类,那么算法认为所有文档都被正确分类,那么purity值为1!而这显然不是想要的结果。
四、RI评价法:
实际上这是一种用排列组合原理来对聚类进行评价的手段,公式如下:
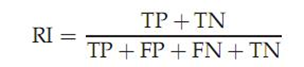
其中TP是指被聚在一类的两个文档被正确分类了,TN是只不应该被聚在一类的两个文档被正确分开了,FP只不应该放在一类的文档被错误的放在了一类,FN指不应该分开的文档被错误的分开了。对上图
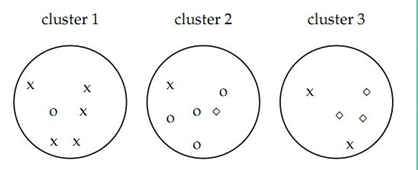
TP+FP = C(2,6) + C(2,6) + C(2,5) = 15 + 15 + 10 = 40
其中C(n,m)是指在m中任选n个的组合数。
TP = C(2,5) + C(2,4) + C(2,3) + C(2,2) = 20
FP = 40 - 20 = 20
同理:
TN+FN= C(1,6) * C(1,6)+ C(1,6)* C(1,5) + C(1,6)* C(1,5)=96
FN= C(1,5) * C(1,3)+ C(1,1)* C(1,4) + C(1,1)* C(1,3)+ C(1,1)* C(1,2)=24
TN=96-24=72
所以RI = ( 20 + 72) / ( 20 + 20 + 72 +24) = 0.68
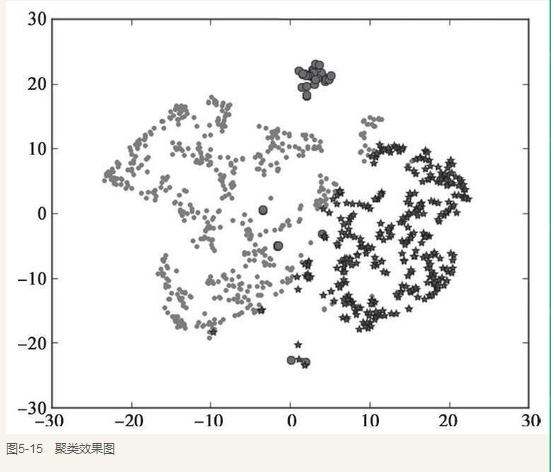
四、聚类分析结果的降维可视化—TSNE
我们总喜欢能够直观地展示研究结果,聚类也不例外。然而,通常来说输入的特征数是高维的(大于3维),一般难以直接以原特征对聚类结果进行展示。而TSNE提供了一种有效的数据降维方式,让我们可以在2维或者3维的空间中展示聚类结果。
示例代码:接上文示例代码
#-*- coding: utf-8 -*-
#接k_means.py
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit_transform(data_zs) #进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index = data_zs.index) #转换数据格式
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
#不同类别用不同颜色和样式绘图
d = tsne[r[u'聚类类别'] == 0]
plt.plot(d[0], d[1], 'r.')
d = tsne[r[u'聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')
d = tsne[r[u'聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')
plt.show()
参考资料
