【4.5.2】验证曲线--绘制验证曲线

在我们在示例中看到的简单的一维问题中，很容易看出估计器是否存在偏差或方差。 然而，在高维空间中，模型可能变得非常难以可视化。 因此，使用验证曲线与学习曲线描述的工具通常很有帮助

为了验证模型，我们需要评分函数（参见模型评估：量化预测的质量，Model evaluation: quantifying the quality of predictions），例如分类器的准确性。 选择估计器的多个超参数的正确方法当然是网格搜索或类似方法（参见调整估计器的超参数，Tuning the hyper-parameters of an estimator），其选择在验证集或多个验证集上具有最大分数的超参数。 请注意，如果我们根据验证分数优化超参数，则验证分数会有偏差，而不再是对泛化的良好估计。 为了得到对泛化的正确估计，我们必须在另一个测试集上计算得分。

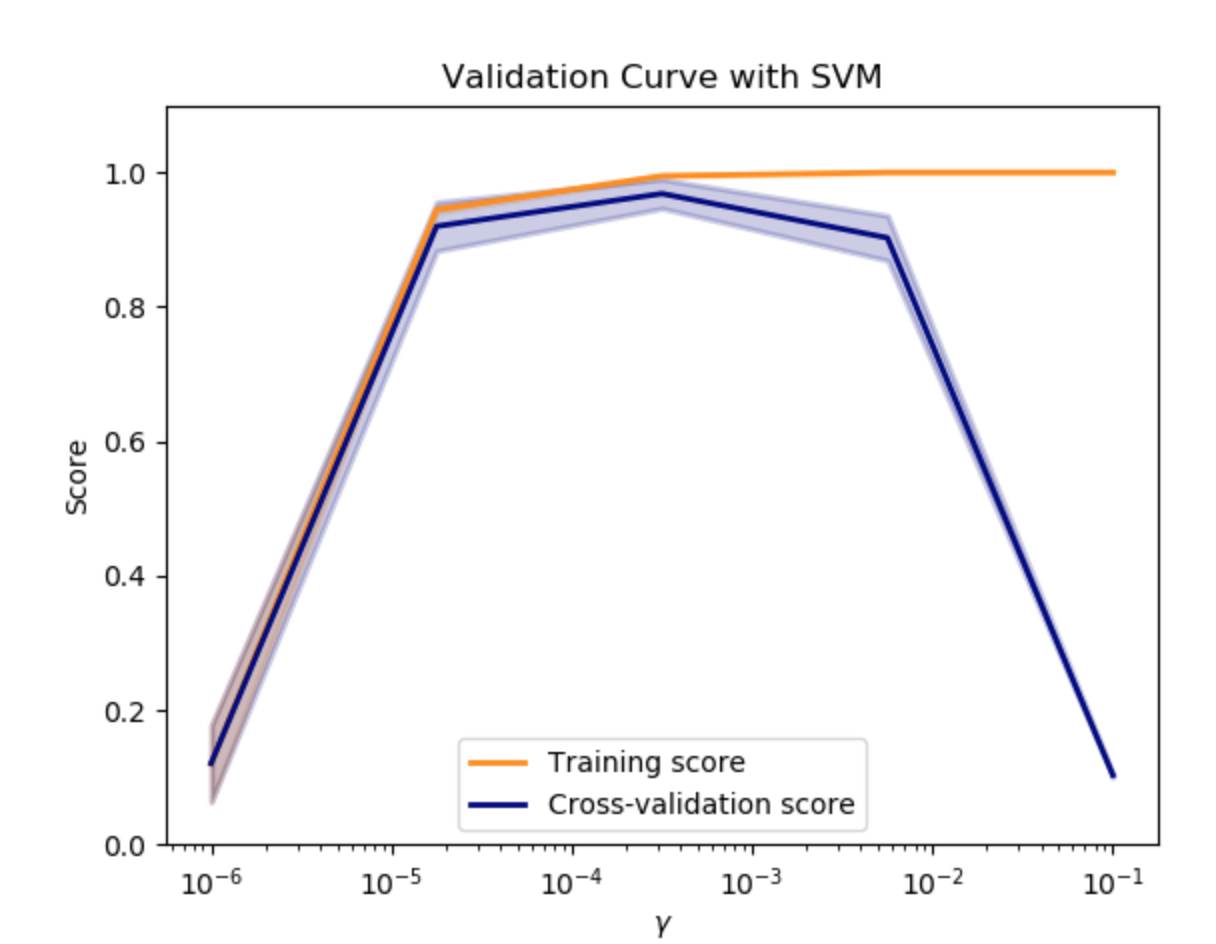
在此图中，您可以查看SVM的训练分数和验证分数，以获取内核参数gamma的不同值。 对于非常低的伽玛值，您可以看到训练分数和验证分数都很低。 这被称为欠配合。 gamma的中值将导致两个分数的高值，即分类器表现得相当好。 如果gamma太高，则分类器将过度拟合，这意味着训练分数良好但验证分数较差。

然而，绘制单个超参数对训练分数和验证分数的影响有时是有帮助的，以确定估计量是否过度拟合或不适合某些超参数值。

• 如果训练分数和验证分数都很低，则估算器将不合适。
• 如果训练分数高且验证分数低，则估计器过度拟合，否则其工作得很好。

通常不可能获得较低的训练分数和较高的验证分数。 所有三种情况都可以在下面的图中找到，我们在数字数据集上改变SVM的参数 $ \gamma$。

代码：

print(__doc__)

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import validation_curve

digits = load_digits()
X, y = digits.data, digits.target

param_range = np.logspace(-6, -1, 5)
train_scores, test_scores = validation_curve(
    SVC(), X, y, param_name="gamma", param_range=param_range,
    cv=10, scoring="accuracy", n_jobs=1)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)

plt.title("Validation Curve with SVM")
plt.xlabel("$\gamma$")
plt.ylabel("Score")
plt.ylim(0.0, 1.1)
lw = 2
plt.semilogx(param_range, train_scores_mean, label="Training score",
             color="darkorange", lw=lw)
plt.fill_between(param_range, train_scores_mean - train_scores_std,
                 train_scores_mean + train_scores_std, alpha=0.2,
                 color="darkorange", lw=lw)
plt.semilogx(param_range, test_scores_mean, label="Cross-validation score",
             color="navy", lw=lw)
plt.fill_between(param_range, test_scores_mean - test_scores_std,
                 test_scores_mean + test_scores_std, alpha=0.2,
                 color="navy", lw=lw)
plt.legend(loc="best")
plt.show()

validation_curve函数实例

import numpy as np
from sklearn.model_selection import validation_curve
from sklearn.datasets import load_iris
from sklearn.linear_model import Ridge

np.random.seed(0)
iris = load_iris()
X, y = iris.data, iris.target
indices = np.arange(y.shape[0])
np.random.shuffle(indices)
X, y = X[indices], y[indices]

train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
                                              np.logspace(-7, 3, 3))
print train_scores           

print valid_scores           

结果：

>>> train_scores           
array([[ 0.94...,  0.92...,  0.92...],
       [ 0.94...,  0.92...,  0.92...],
       [ 0.47...,  0.45...,  0.42...]])
>>> valid_scores           
array([[ 0.90...,  0.92...,  0.94...],
       [ 0.90...,  0.92...,  0.94...],
       [ 0.44...,  0.39...,  0.45...]])

参考资料

• http://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.html#sphx-glr-auto-examples-model-selection-plot-validation-curve-py
• http://scikit-learn.org/stable/modules/learning_curve.html