【2】监督学习--2--回归
一、基本概念
回归:统计学分析数据的方法,目的在于了解两个或多个变数间是否相关、 研究其相关方向与强度,并建立数学模型以便观察特定变数来预测研究者感兴 趣的变数。回归分析可以帮助人们了解在自变量变化时因变量的变化量。一般 来说,通过回归分析我们可以由给出的自变量估计因变量的条件期望。
Generalized Linear Models ( 广义线性模型 )
以下是一组用于回归的方法,他们的目标值是输入变量的线性组合。假设数学符号 $\hat{y}$表示预测值。
$$\hat{y}(w,x) = wo + w_{1}x_{1} + w_{2}x_{2} +w_{3}x_{3} +... +w_{p}x_{p} $$
在整个模块中,我们指定coef_ 代表向量 $w = { w_{1},...w_{p}}$, intercept_ 代表w_0 。
要使用广义线性回归进行分类,请参阅 Logistic 回归。
Sklearn vs. 回归
Sklearn提供的回归函数主要被封装在两个子模块中,分别是 sklearn.linear_model和sklearn.preprocessing。
sklearn.linear_modlel封装的是一些线性函数,线性回归函数包括有:
- 普通线性回归函数( LinearRegression )
- 岭回归(Ridge)
- Lasso(Lasso)
非线性回归函数,如多项式回归(PolynomialFeatures)则通过 sklearn.preprocessing子模块进行调用
二、回归应用
回归方法适合对一些带有时序信息的数据进行预测或者趋势拟合,常用在 金融及其他涉及时间序列分析的领域:
- 股票趋势预测
- 交通流量预测
三、具体案例
3.1 线性回归(Linear Regression)
是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分 析方法。
线性回归利用称为线性回归方程的最小平方函数对一个或多个自 变量和因变量之间关系进行建模。这种函数是一个或多个称为回 归系数的模型参数的线性组合。只有一个自变量的情况称为简单 回归,大于一个自变量情况的叫做多元回归。
线性回归:使用形如y=wTx+b 的线性模型拟合数据输入和输出之 间的映射关系的。
线性回归的实际用途
线性回归有很多实际的用途,分为以下两类:
- 如果目标是预测或者映射,线性回归可以用来对观测数据集的y和X 的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值, 在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个 y值。
- 给定一个变量y和一些变量X , ⋯ ,𝑋,这些变量有可能与y相关,回归分析可以用来量化y与X之间相关性的强度,评估出与y不相关的Xj,并识别出哪些子集包含了关于y的冗余信息。
线性回归的应用
背景:与房价密切相关的除了单位的房价,还有房屋的尺寸。我们可以根 据已知的房屋成交价和房屋的尺寸进行线性回归,继而可以对已知房屋尺 寸,而未知房屋成交价格的实例进行成交价格的预测
目标:对房屋成交信息建立回归方程,并依据回归方程对房屋价格进行预测 技术路线:sklearn.linear_model.LinearRegression
实例数据
为了方便展示,成交信息只使用 了房屋的面积以及对应的成交价格。 其中:
- 房屋面积单位为平方英尺(ft2)房
- 屋成交价格单位为万
可行性分析
- 简单而直观的方式是通过数据的可视化直接观察房屋成交价格与房 屋尺寸间是否存在线性关系。
- 对于本实验的数据来说,散点图就可以很好的将其在二维平面中进 行可视化表示。
右图为数据的散点图,其中横坐 标为房屋面积,纵坐标为房屋的成 交价格。可以看出,靠近坐标左下 角部分的点,表示房屋尺寸较小的 房子,其对应的房屋成交价格也相 对较低。同样的,靠近坐标右上部 分的点对应于大尺寸高价格的房 屋。从总体来看,房屋的面积和成 交价格基本成正比。
实验过程
使用算法:线性回归 实现步骤:
- 建立工程并导入sklearn包
- 加载训练数据,建立回归方程
- 可视化处理
代码:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
# 读取数据集
datasets_X = []
datasets_Y = []
fr = open('prices.txt','r')
lines = fr.readlines()
for line in lines:
items = line.strip().split(',')
datasets_X.append(int(items[0]))
datasets_Y.append(int(items[1]))
length = len(datasets_X)
datasets_X = np.array(datasets_X).reshape([length,1])
datasets_Y = np.array(datasets_Y)
minX = min(datasets_X)
maxX = max(datasets_X)
X = np.arange(minX,maxX).reshape([-1,1])
linear = linear_model.LinearRegression()
linear.fit(datasets_X, datasets_Y)
调用sklearn.linear_model.LinearRegression()所需参数:
fit_intercept : 布尔型参数,表示是否计算该模型截距。可选参数。
normalize : 布尔型参数,若为True,则X在回归前进行归一化。可选参数。默认值为False。
copy_X : 布尔型参数,若为True,则X将被复制;否则将被覆盖。可选参数。默认值为True。
n_jobs : 整型参数,表示用于计算的作业数量;若为-1,则用所有的CPU。可选参数。默认值为1。
* * *
线性回归fit函数用于拟合输入输出数据,调用形式为linear.fit(X,y, sample_weight=None): X : X为训练向量;
y : y为相对于X的目标向量;
sample_weight : 分配给各个样本的权重数组,一般不需要使用,可省略。
# 图像中显示
plt.scatter(datasets_X, datasets_Y, color = 'red')
plt.plot(X, linear.predict(X), color = 'blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()
多项式回归
-
多项式回归(Polynomial Regression)是研究一个因变量与一 个或多个自变量间多项式的回归分析方法。如果自变量只有一个 时,称为一元多项式回归;如果自变量有多个时,称为多元多项 式回归。
-
一元m次多项式回归方程为:
-
二元二次多项式回归方程为:
-
在一元回归分析中,如果依变量y与自变量x的关系为非线性的,但 是又找不到适当的函数曲线来拟合,则可以采用一元多项式回归。 多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼近,直至满意为止。
-
事实上,多项式回归可以处理相当一类非线性问题,它在回归分析 中占有重要的地位,因为任一函数都可以分段用多项式来逼近。
应用背景:我们在前面已经根据已知的房屋成交价和房屋的尺寸进行了线 性回归,继而可以对已知房屋尺寸,而未知房屋成交价格的实例进行了成 交价格的预测,但是在实际的应用中这样的拟合往往不够好,因此我们在 此对该数据集进行多项式回归。
目标:对房屋成交信息建立多项式回归方程,并依据回归方程对房屋价格进行预测
技术路线:sklearn.preprocessing.PolynomialFeatures
实例数据
成交信息包括房屋的面积以及对 应的成交价格:
- 房屋面积单位为平方英尺(ft2)
- 房屋成交价格单位为万
代码:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# 读取数据集
datasets_X = []
datasets_Y = []
fr = open('prices.txt','r')
lines = fr.readlines()
for line in lines:
items = line.strip().split(',')
datasets_X.append(int(items[0]))
datasets_Y.append(int(items[1]))
length = len(datasets_X)
datasets_X = np.array(datasets_X).reshape([length,1])
datasets_Y = np.array(datasets_Y)
minX = min(datasets_X)
maxX = max(datasets_X)
X = np.arange(minX,maxX).reshape([-1,1])
poly_reg = PolynomialFeatures(degree = 2)
X_poly = poly_reg.fit_transform(datasets_X)
lin_reg_2 = linear_model.LinearRegression()
lin_reg_2.fit(X_poly, datasets_Y)
sklearn中多项式回归: 这里的多项式回归实际上是先将变量X处理成多项式特征,然后使用线性模型学
习多项式特征的参数,以达到多项式回归的目的。 例如:X = [x1, x2]
1.使用PolynomialFeatures构造X的二次多项式特征X_Poly:
X_Poly = [x1, x2, x1x2, x2*x2, x1*x1]
2.使用linear_model学习X_Poly和y之间的映射关系,即参数:
w1x1 + w2x2 +w3x1x2 +w4x1x1+w5x2x2 = y
degree=2表示建立datasets_X的二 次多项式特征X_poly。然后创建线 性回归,使用线性模型学习X_poly 和datasets_Y之间的映射关系(即 参数)。
# 图像中显示
plt.scatter(datasets_X, datasets_Y, color = 'red')
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()
3.1 岭回归
解决传统的基于最小二乘的线性回归法缺乏稳定性。
。。。公式略
岭回归(ridge regression)是一种专用于共线性数据分析的有偏估计回归方法 是一种改良的最小二乘估计法,对某些数据的拟合要强于最小二乘法。 在sklearn库中,可以使用sklearn.linear_model.Ridge调用岭回归模型,其 主要参数有:
- alpha:正则化因子,对应于损失函数中
- fit_intercept:表示是否计算截距
- solver:设置计算参数的方法,可选参数‘auto’、‘svd’、‘sag’等
交通流量预测实例
数据介绍:
交通流量预测实例 数据为某路口的交通流量监测数据,记录全年小时级别的车流量。
实验目的:
根据已有的数据创建多项式特征,使用岭回归模型代替一般的线性模型,对车流量的信息进行多项式回归。
技术路线:sklearn.linear_model.Ridgefrom sklearn.preprocessing.PolynomialFeatures
1.建立工程,导入sklearn相关工具包
>> import numpy as np
>>> from sklearn.linear_model import Ridge #通过sklearn.linermodel加载岭回归方法
>>> from sklearn import cross_validation #加载交叉验证模块,加载matplotilib模块
>>> import matplotlib.pyplot as plt
>>> from sklearn.preprocessing import PolynomialFeatures #通过。。加载。。。用于创建多项式特征,如ab、a2、b2
2.数据加载:
data=np.genfromtxt('data.txt') #使用numpy的方法从txt文件中加载数据 >>> plt.plot(data[:,4]) #使用plt展示车流量信息,如右图
3.数据处理:
ata[:,:4]
#X用于保存0-3维数据,即属性
>>> y=data[:,4]
#y用于保存第4维数据,即车流量
>>> poly=PolynomialFeatures(6) #用于创建最高次数6次方的的多项式特征,多次试验后决定采用6次 >>> X=poly.fit_transform(X)
#X为创建的多项式特征
4.划分训练集和测试集:
>>> train_set_X, test_set_X , train_set_y, test_set_y = cross_validation.train_test_split(X,y,test_size=0.3,
random_state=0)
#将所有数据划分为训练集和测试集,test_size表示测试集的比例, #random_state是随机数种子
5.创建回归器,并进行训练:
>>> clf=Ridge(alpha=1.0,fit_intercept = True) #接下来我们创建岭回归实例
>>> clf.fit(train_set_X,train_set_y) #调用fit函数使用训练集训练回归器
>>> clf.score(test_set_X,test_set_Y) #利用测试集计算回归曲线的拟合优度,clf.score返回值为0.7375 #拟合优度,用于评价拟合好坏,最大为1,无最小值,当对所有输入都输 出同一个值时,拟合优度为0。
6.画出拟合曲线:
>>> start=200 #接下来我们画一段200到300范围内的拟合曲线
>>> end=300
>>> y_pre=clf.predict(X) #是调用predict函数的拟合值
>>> time=np.arange(start,end)
>>> plt.plot(time,y[start:end],'b', label="real")
>>> plt.plot(time,y_pre[start:end],'r', label='predict') #展示真实数据(蓝色)以及拟合的曲线(红色)
>>> plt.legend(loc=‘upper left’) #设置图例的位置
>>> plt.show()
分析结论:预测值和实际值的走势大致相同
四、各种概念
1.Ordinary Least Squares ( 普通最小二乘法 )
LinearRegression类 拟合系数为$w = { w_{1},…w_{p}}$`的线性模型, 来最小化,样本集中观测点和线性近似的预测点之间的残差平方和。
其实就是解决如下的一个数学问题:
$$ \min \limits_{w}\||Xw - y ||_{2}^{2}$$
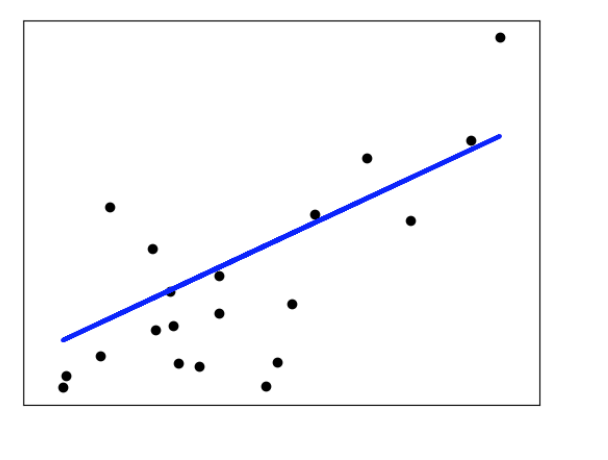
LinearRegression类的成员函数 fit 以数组X和y为输入,并将线性模型的系数 w 存储在其成员变量coef_ 中:
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5, 0.5])
然而,最小二乘的系数估计依赖于模型特征项的独立性。当特征项相关并且设计矩阵X 的列近似的线性相关时,设计矩阵便接近于一个奇异矩阵,因此最小二乘估计对观测点中的随机误差变得高度敏感,产生大的方差。例如,当没有试验设计的收集数据时,可能会出现这种多重共线性(multicollinearity )的情况
Ordinary Least Squares Complexity ( 普通最小二乘法复杂度 )
该方法通过对X进行 singular value decomposition ( 奇异值分解 ) 来计算最小二乘法的解。如果 X 是大小为 O(n, p) 的矩阵,则该方法的复杂度为 ,假设 n≥p 。
###2. Ridge Regression ( 岭回归 )
岭回归通过对系数的大小施加惩罚来解决 普通最小二乘 的一些问题。 ridge coefficients ( 岭系数 ) 最小化一个带罚项的残差平方和,
$$ \min \limits_{w}\||Xw - y ||_{2}^{2} + α||w||_{2}^{2}$$
这里,α ≥0 是控制缩减量的复杂度参数:α值越大,缩减量越大,因此系数变得对共线性变得更加鲁棒。
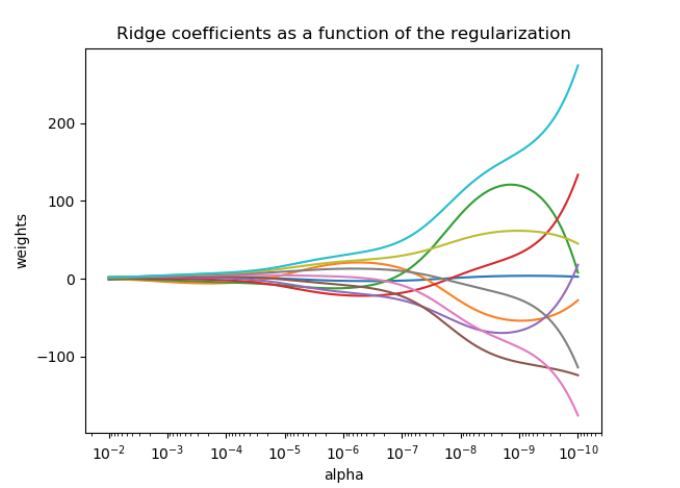
与其他线性模型一样,Ridge 类成员函数 fit 以数组X和y为输入,并将线性模型的系数 w 存储在其成员变量coef_ 中:
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...
Ridge Complexity ( 岭复杂性 ):
这种方法与 Ordinary Least Squares ( 普通最小二乘方法 ) 的复杂度相同
Setting the regularization parameter: generalized Cross-Validation ( 设置正则化参数:广义交叉验证 )
RidgeCV 通过内置的 Alpha 参数的交叉验证来实现岭回归。 该对象的工作方式与 GridSearchCV 相同,只是它默认为 Generalized Cross-Validation ( 通用交叉验证 ) (GCV),这是一种有效的留一交叉验证法:
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None,
normalize=False)
>>> reg.alpha_
0.1
3.Lasso
Lasso 是估计稀疏系数的线性模型。它在一些情况下是有用的,因为它倾向于使用具有较少参数值的解决方案,有效地减少给定解决方案所依赖的变量的数量。为此,Lasso 及其变体是 compressed sensing ( 压缩感测领域 ) 的基础。在某些条件下,它可以恢复精确的非零权重集(参见 Compressive sensing: tomography reconstruction with L1 prior (Lasso) ( 压缩感测:使用 L1 先验( Lasso )进行断层扫描重建 ) )。
在数学上,它由一个使用l1先验作为正则化项的线性模型组成。最小化的目标函数是:
$$ \min \limits_{w}\ \frac{1}{2n_{samples}}||Xw - y ||_{2}^{2} + α||w||_{1}$$
因此,lasso estimate 解决了加上罚项 $α||w||_{1}$ 的最小二乘法的最小化,其中,α常数, $||w||_{1}$是参数向量l1的范数 。
Lasso 类中的实现使用坐标下降作为算法来拟合系数。查看 Least Angle Regression ( 最小角度回归 ) 用于另一个实现
>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha = 0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection='cyclic', tol=0.0001, warm_start=False)
>>> reg.predict([[1, 1]])
array([ 0.8])
对于较低级别的任务也很有用的是函数 lasso_path 来计算可能值的完整路径上的系数。
4.Multi-task Lasso ( 多任务套索 )
个二维数组,shape(n_samples,n_tasks)。约束是所选的特征对于所有的回归问题都是相同的,也称为 tasks ( 任务 )。
下图比较了使用简单 Lasso 或 MultiTaskLasso 获得的 W 中非零的位置。 Lasso 估计产生分散的非零,而 MultiTaskLasso 的非零是全列。
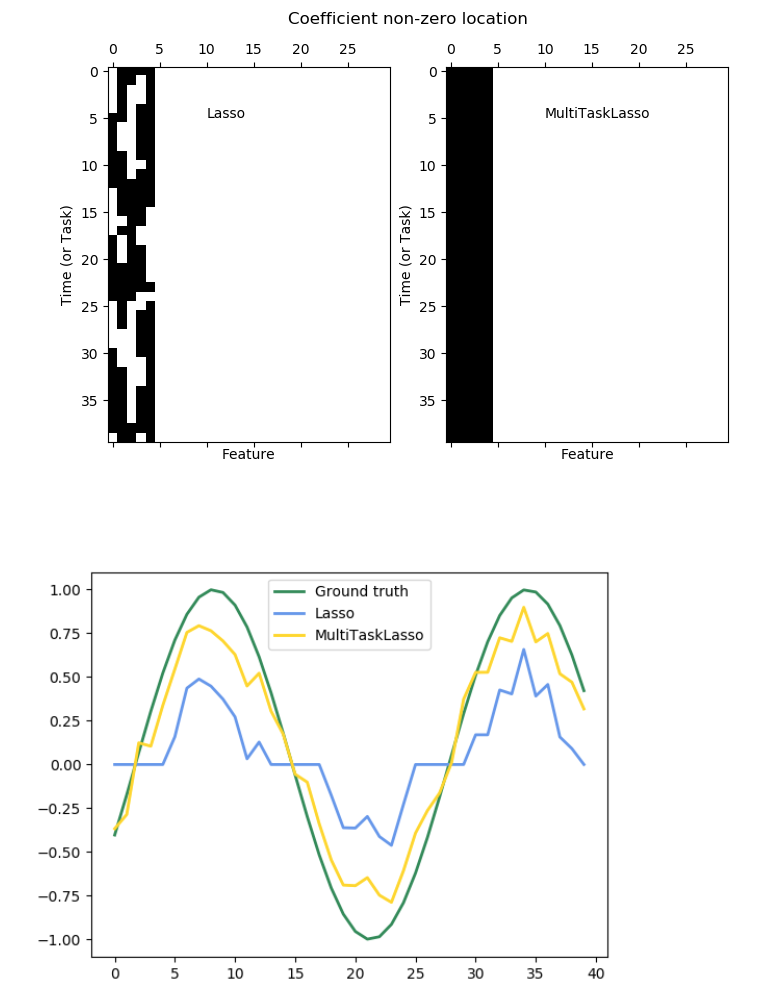
拟合 time-series model ( 时间序列模型 ),强制任何活动的功能始终处于活动状态。
在数学上,它由一个线性模型组成,训练有混合的l1 l2 之前的正则化。目标函数最小化是:
$$ \min \limits_{w}\ \frac{1}{2n_{samples}}||XW - Y ||_{Fro}^{2} + α||W||_{21}$$
其中 Fro表示 Frobenius 规范:
$$ ||A||_{Fro}^{2} = \sqrt{\sum_{ij}a_{ij}^{2}} $$
和l1 l2读取:
$$ ||A||_{21}^{2} = \sum_{i}\sqrt{\sum_{j}a_{ij}^{2}} $$
… 东西太多,有些迷糊了,后面再来整理。。。
4.Bayesian Regression ( 贝叶斯回归 )
贝叶斯回归技术可以用于在估计过程中包括正则化参数:正则化参数不是硬的设置,而是调整到手头的数据。
为了获得一个完全概率模型,输出y被假定为高斯分布在 Xw 周围:
$$p(y|X,w,α) = N(y| X w, α)$$
Alpha 再次被视为从数据估计的随机变量。
贝叶斯回归的优点是:
- 它适应了 data at hand ( 手头的数据 ) 。
- 它可以用于在估计过程中包括正则化参数。
贝叶斯回归的缺点包括:
模型的推论可能是耗时的。
贝叶斯回归用于回归:
>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge(alpha_1=1e-06, alpha_2=1e-06, compute_score=False, copy_X=True,
fit_intercept=True, lambda_1=1e-06, lambda_2=1e-06, n_iter=300,
normalize=False, tol=0.001, verbose=False)
安装后,该模型可用于预测新值:
>>> reg.predict ([[1, 0.]])
array([ 0.50000013])
模型的权重 w 可以访问:
>>> reg.coef_
array([ 0.49999993, 0.49999993])
由于贝叶斯框架,发现的权重与普通最小二乘法发现的权重略有不同。然而,贝叶斯岭回归对于不适当的问题更为强大。
5. Polynomial regression: extending linear models with basis functions ( 多项式回归:用基函数扩展线性模型 )
机器学习中的一种常见模式是使用训练数据非线性函数的线性模型。这种方法保持线性方法的 generally fast performance ( 一般快速性能 ) ,同时允许它们适应更广泛的数据。
例如,可以通过从 constructing polynomial features ( 系数构造多项式特征 ) 来扩展简单的线性回归。在标准线性回归的情况下,您可能有一个类似于二维数据的模型:
$$\hat{y}(w,x) = wo + w_{1}x_{1} + w_{2}x_{2} $$
如果我们想要将数学拟合为抛物面而不是平面,我们可以将 second-order polynomials ( 二阶多项式 ) 的特征组合起来,使得模型如下所示:
$$\hat{y}(w,x) = wo + w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{1}x_{2}+ w_{4}x_{1}^{2}+ w_{5}x_{2}^{2} $$
(有时令人惊讶)的观察是,这仍然是一个线性模型:要看到这一点,想象一下创建一个新的变量:
$$z= [x_{1},x_{2},x_{1}x_{2},x_{1}^{2},x_{2}^{2}]$$
通过对数据的重新标注,可以写出我们的问题
$$\hat{y}(w,x) = wo + w_{1}z_{1} + w_{2}z_{2}+ w_{3}z_{3} + w_{4}z_{4} + w_{5}z_{5} $$
我们看到所得到的多项式回归与上面我们考虑过的线性模型相同(即模型在 w 中是线性的),并且可以通过相同的技术来解决。通过考虑使用这些基本功能构建的更高维度空间内的线性拟合,该模型具有适应更广泛范围的数据的灵活性。
以下是使用不同程度的多项式特征将这一想法应用于一维数据的示例:
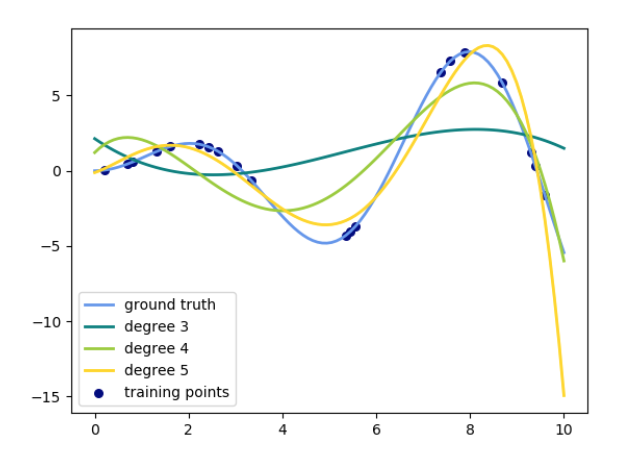
该图是使用 PolynomialFeatures 预处理器创建的。该预处理器将输入数据矩阵转换为给定度的新数据矩阵。它可以使用如下:
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
X 的特征已经从[x1,x2]转换为[1,x1,x2,x1^2,x1x2,x2^2] ,现在可以在任何线性模型中使用。degree=2代表指数设置为2 。这种预处理可以使用 Pipeline 进行简化。可以创建表示简单多项式回归的单个对象,并使用如下
>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
... ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2., 1., -1.])
训练多项式特征的线性模型能够准确地恢复输入多项式系数。
在某些情况下,没有必要包含任何单个功能的更高的功能,而只包含所有交互功能,这些功能可以在多达 d 个不同的功能中进行叠加。这些可以通过设置 interaction_only = True 从 PolynomialFeatures 获得。
例如,当处理布尔特征时,所有 n 的$x_{i}^{n} = x_{i}$, 因此是无用的;但 $x_{i} x_{j}$ 表示两个布尔值的连接。这样,我们可以使用线性分类器来解决 XOR 问题:
>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
[1, 0, 1, 0],
[1, 1, 0, 0],
[1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, n_iter=10, shuffle=False).fit(X, y)
And the classifier “predictions” are perfect: ( 分类器“预测”是完美的 ) :
>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0
6. 其他略。。。
参考资料
