【2】监督学习--1--分类-支持向量机(svm)
简单点讲,SVM就是一种二类分类模型,他的基本模型是的定义在特征空间上的间隔最大的线性分类器,SVM的学习策略就是间隔最大化。
一、基本概念
支持向量机 (SVM) 是一种相对简单的监督机器学习算法,用于解决分类或回归问题。它更适合分类,但有时对回归也非常有用。SVM算法的本质是在不同的数据类型之间找到一个超平面来创建边界。在二维空间中,这个超平面是一条直线。
在 SVM算法中,我们在 N 维空间中绘制数据集中的每个数据项,其中 N 是数据中特征/属性的数量。接下来,我们找到最佳的超平面来对不同类型的数据进行分类。因此我们可以了解到SVM 本质上只能解决二分类的问题(即,在两个类之间进行选择)。但是,如今有多种技术可用于解决多分类的问题。
1.1 直观理解

图中有分别属于两类的一些二维数据点和三条直线。如果三条直线分别代表三个分类器的话,请问哪一个分类器比较好?
我们凭直观感受应该觉得答案是H3。首先H1不能把类别分开,这个分类器肯定是不行的;H2可以,但分割线与最近的数据点只有很小的间隔,如果测试数据有一些噪声的话可能就会被H2错误分类(即对噪声敏感、泛化能力弱)。H3以较大间隔将它们分开,这样就能容忍测试数据的一些噪声而正确分类,是一个泛化能力不错的分类器。
对于支持向量机来说,数据点若是图片维向量,我们用图片维的超平面来分开这些点。但是可能有许多超平面可以把数据分类。最佳超平面的一个合理选择就是以最大间隔把两个类分开的超平面。因此,SVM选择能够使离超平面最近的数据点的到超平面距离最大的超平面。
以上介绍的SVM只能解决线性可分的问题,为了解决更加复杂的问题,支持向量机学习方法有一些由简至繁的模型:
- 线性可分SVM: 当训练数据线性可分时,通过硬间隔(hard margin,什么是硬、软间隔下面会讲)最大化可以学习得到一个线性分类器,即硬间隔SVM,如上图的的H3。
- 线性SVM: 当训练数据不能线性可分但是可以近似线性可分时,通过软间隔(soft margin)最大化也可以学习到一个线性分类器,即软间隔SVM。
- 非线性SVM: 当训练数据线性不可分时,通过使用核技巧(kernel trick)和软间隔最大化,可以学习到一个非线性SVM。
线性可分SVM——硬间隔
在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量(support vector)
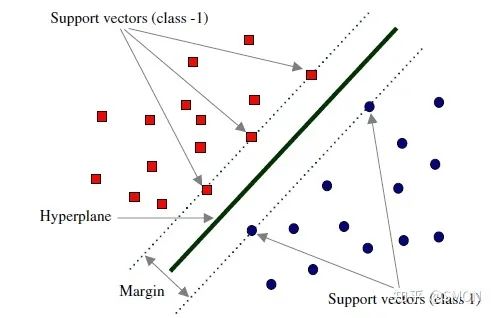
在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用(具体推导见2.4节最后)。如果移动非支持向量,甚至删除非支持向量都不会对最优超平面产生任何影响。也即支持向量对模型起着决定性的作用,这也是“支持向量机”名称的由来。
线性SVM——软间隔
在前面的讨论中,我们一直假定训练数据是严格线性可分的,即存在一个超平面能完全将两类数据分开。但是现实任务这个假设往往不成立,例如下图所示的数据。
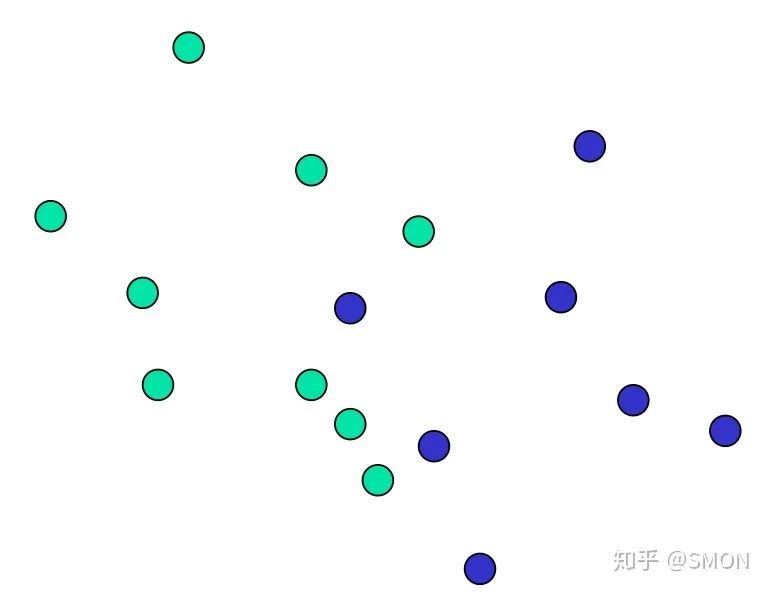
解决该问题的一个办法是允许SVM在少量样本上出错,即将之前的硬间隔最大化条件放宽一点,为此引入“软间隔(soft margin)”的概念。即允许少量样本不满足约束
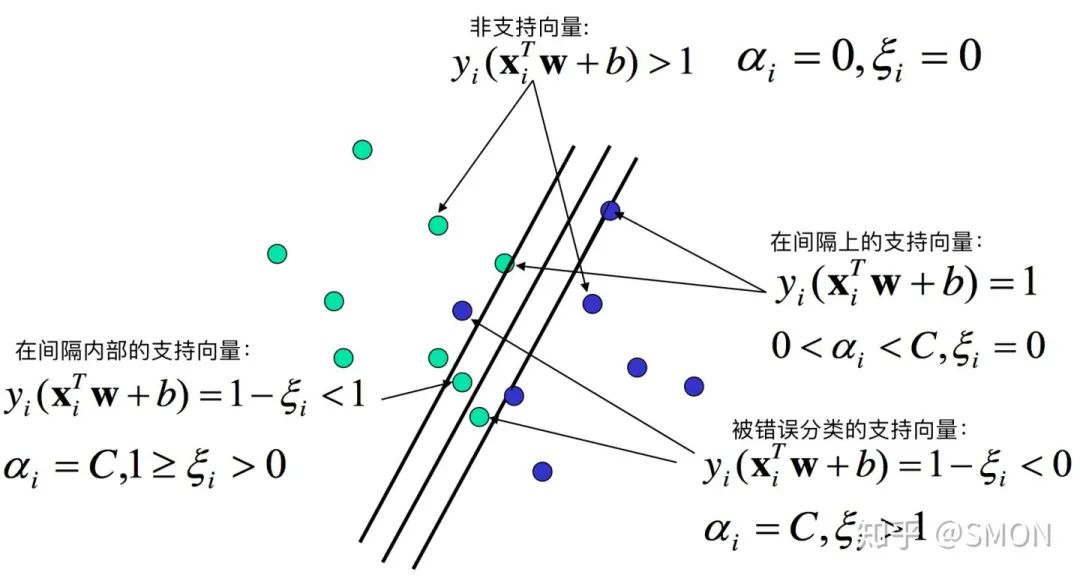
因此,我们有与2.4节相同的结论,最优超平面只与支持向量有关而与非支持向量无关。
非线性SVM——核技巧
前面介绍的都是线性问题,但是我们经常会遇到非线性的问题(例如异或问题),此时就需要用到核技巧(kernel trick)将线性支持向量机推广到非线性支持向量机。需要注意的是,不仅仅是SVM,很多线性模型都可以用核技巧推广到非线性模型,例如核线性判别分析(KLDA)。
如下图所示,核技巧的基本思路分为两步:使用一个变换将原空间的数据映射到新空间(例如更高维甚至无穷维的空间);然后在新空间里用线性方法从训练数据中学习得到模型。
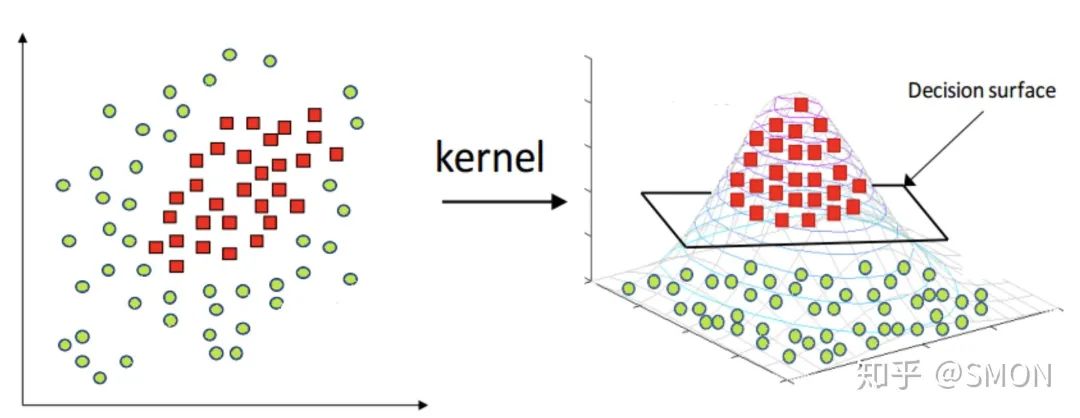
1.4 优缺点
任何算法都有其优缺点,支持向量机也不例外。
支持向量机的优点是:
- 由于SVM是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优。
- 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
- 拥有高维样本空间的数据也能用SVM,这是因为数据集的复杂度只取决于支持向量而不是数据集的维度,这在某种意义上避免了“维数灾难”。
- 理论基础比较完善(例如神经网络就更像一个黑盒子)。
支持向量机的缺点是:
- 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)
- 只适用于二分类问题。(SVM的推广SVR也适用于回归问题;可以通过多个SVM的组合来解决多分类问题)
三、案例
3.2 案例1
首先我们用sklearn包自带的方法创建两组数据集:
# importing scikit learn with make_blobs
from sklearn.datasets.samples_generator import make_blobs
# creating datasets X contarining n_samples
# Y containing two classes
X,Y = make_blobs(n_samples=500, centers=2,
random_state=0, cluster_std=0.40)
import matplotlib.pyplot as plt
# plotting scatters
plt.scatter(X[:,0], X[:, 1], c=Y, s=50, cmap='spring');
plt.show()
创建后的数据集可视化如下图:
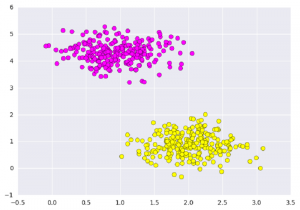
SVM不仅是在此处在两个类之间画一条线,而且还要考虑某个给定宽度的线周围的区域。下面是它的外观示例:
# creating line space between -1 to 3.5
xfit = np.linspace(-1, 3.5)
# plotting scatter
plt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='spring')
# plot a line between the different sets of data
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
plt.show()
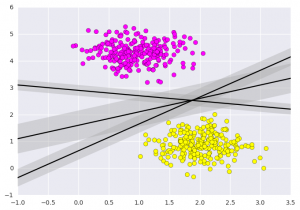
以上是支持向量机的直觉,它优化了表示数据集之间垂直距离的线性判别模型。现在让我们使用我们的训练数据训练分类器。在训练之前,我们需要将癌症数据集导入为 csv 文件,我们将从所有特征中训练两个特征。
# importing required libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# reading csv file and extracting class column to y.
x = pd.read_csv("C:\...\cancer.csv")
a = np.array(x)
y = a[:,30] # classes having 0 and 1
# extracting two features
x = np.column_stack((x.malignant,x.benign))
# 569 samples and 2 features
x.shape
print (x),(y)
现在我们将利用这些点来拟合SVM分类器。虽然似然模型的数学细节很有趣,但我们将在别处阅读这些细节。相反,我们只是将scikit-learn 算法视为完成上述任务的黑匣子。
# import support vector classifier
# "Support Vector Classifier"
from sklearn.svm import SVC
clf = SVC(kernel='linear')
# fitting x samples and y classes
clf.fit(x, y)
拟合完成后,该模型可用于预测新值:
clf.predict([[120, 990]])
clf.predict([[85, 550]])
输出:
array([ 0.])
array([ 1.])
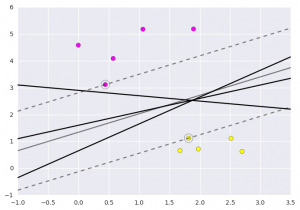
我们可以通过 matplotlib 分析获取的数据和预处理方法以制作最佳超平面的过程。
3.2 案例:上证指数涨跌预测
数据介绍:
上证指数涨跌预测 网易财经上获得的上证指数的历史数据,爬取了20年的上证指数数据。 实验目的: 根据给出当前时间前150天的历史数据,预测当天上证指数的涨跌。
技术路线:sklearn.svm.SVC
import pandas as pd
import numpy as np
from sklearn import svm
from sklearn import cross_validation
data=pd.read_csv('stock/000777.csv',encoding='gbk',parse_dates=[0],index_col=0) #(数据源, encoding=编码格式为gbk, parse_dates=第0列解析为日期, index_col= 用作行索引的列编号)
data.sort_index(0,ascending=True,inplace=True) #详细解释( http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.sort_index.html ) DataFrame.sort_index(axis=0 (按0列排), ascending=True(升序), inplace=False(排序后是否覆盖原 数据))data 按照时间升序排列
dayfeature=150
featurenum=5*dayfeature
x=np.zeros((data.shape[0]-dayfeature,featurenum+1))
y=np.zeros((data.shape[0]-dayfeature))
#参数解释:
选取5列数据作为特征:收盘价 最高价 最低价 开盘价 成交量 dayfeature:选取150天的数据 featurenum:选取的5个特征*天数 x:记录150天的5个特征值
y:记录涨或者跌
data.shape[0]-dayfeature意思是因为我们要用150天数据做训练,对于条目为200条的数据,只有50条数 据是有前150天的数据来训练的,所以训练集的大小就是200-150, 对于每一条数据,他的特征是前150 天的所有特征数据,即150*5, +1是将当天的开盘价引入作为一条特征数据
for i in range(0,data.shape[0]-dayfeature):
x[i,0:featurenum]=np.array(data[i:i+dayfeature] \
[[u'收盘价',u'最高价',u'最低价',u'开盘价',u'成交量']]).reshape((1,featurenum))
x[i,featurenum]=data.ix[i+dayfeature][u'开盘价']
for i in range(0,data.shape[0]-dayfeature):
if data.ix[i+dayfeature][u'收盘价']>=data.ix[i+dayfeature][u'开盘价']:
y[i]=1
else:
y[i]=0
clf=svm.SVC(kernel='rbf') #
//调用svm函数,并设置kernel参数,默认是rbf,其它:‘linear ’‘poly’‘sigmoid’
result = []
for i in range(5):
x_train, x_test, y_train, y_test = \
cross_validation.train_test_split(x, y, test_size = 0.2) #//x和y的验证集和测试集,切分80-20%的测试集
clf.fit(x_train, y_train)
result.append(np.mean(y_test == clf.predict(x_test))) #/将预测数据和测试集的验证数据比对
print("svm classifier accuacy:")
print(result)
四、讨论
4.1 交叉验证 的 基本思想:
交叉验证法先将数据集D划分为k个大小相似的互斥子集,每个自己都尽可能保持数 据分布的一致性,即从D中通过分层采样得到。然后,每次用k-1个子集的并集作为 训练集,余下的那个子集作为测试集;这样就可获得k组训练/测试集,从而可进行k 次训练和测试,最终返回的是这个k个测试结果的均值。通常把交叉验证法称为“k者 交叉验证”, k最常用的取值是10,此时称为10折交叉验证。
参考资料
