【1.4.1】Stata回归结果解读
一、简介
本文使用Stata官方数据auto.dta, 该数据为美国1978年汽车相关数据,对其进行回归分析,对回归的表格相关指标进行详细的解释。 假定模型如下:
$ p r i c e i = α + β 1 m p g i + β 2 w e i g h t i + β 3 l e n g t h i + β 4 t u r n i + β i f o r e i g n i + ε i price_i=\alpha+\beta_ 1mpg_i+\beta_2 weight_i+\beta_3 length_i +\beta_4 turn_i +\beta_i foreign_i +\varepsilon_i $
回归结果如下:
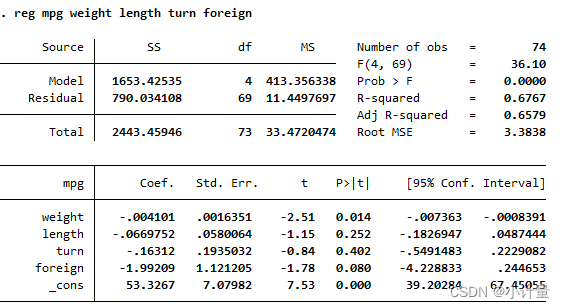
接下来对回归结果报告的各项指标进行解读。
二、指标
将以上的回归结果指标整理成表格。
表1:总体回归结果指标(1)
指标 英文 名称 解释
SS sum of squares 平方和
df degrees of freedom 自由度
MS mean square 均方差
Model(SSM) sum of squares model 模型平方和 衡量预测值的离散程度
Residual(SSR) sum of squares residual 残差平方和 衡量预测值与真实值的偏差程度
Total(SST) sum of squares total 总平方和 衡量真实数据的离散程度
Number of obs 观测值数量 观测值数量
F(a,b) F值 检验系数不为0的概率
Prob > F P值 1%、5%、10%水平上显著
R-squared 拟合系数 表示模型的拟合程度
Adj R-squared 调整后的拟合系数 更精确的表示模型的拟合程度
Root MSE Root Mean square of error 均误差平方根 衡量模型中的误差项的大小
表2:总体回归结果指标(2)
指标 英文名 中文名 解释
Coefficient 系数 模型回归系数
Std. err. The standard error of the coefficient 回归系数标准误 衡量估计值和真实之间差异
t t值 检验系数不为0的概率
p > [t] P值 1%、5%、10%水平上显著
[95% conf. interval] confidence interval 置信区间 回归系数取值范围,该范围有效率是95%
三、详细解释
1、Total(SST):总平方和
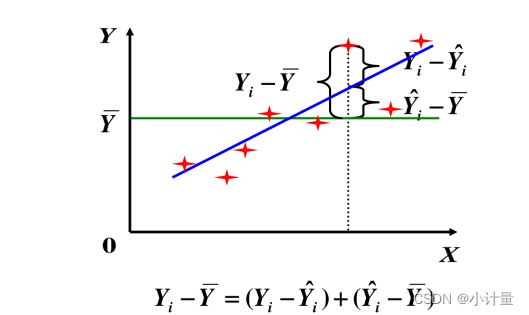
图1:SST、SSR、SSE图
根据图1,可以知道,$ SST=\sum(Y_i -\overline{Y}) $
对应到上文的回归结果中即 $ SST=\sum(price_i -\overline{price}) $ ,即价格的原始数据减去均值。
2、Model(SSM):模型平方和
根据图1,可以知道,$ SSM=\sum(\widehat{Y_i}-\overline{Y}) $
对应到上文的回归结果中即 $ SSM=\sum(\widehat{price_i}-\overline{price})$ ,即价格的预测值减去均值。
3、Residual(SSR):残差平方和
根据图1,可以知道,$ SSR=\sum(Y_i-\widehat{Y_i})$
对应到上文的回归结果中即 $ SSR=\sum(price_i-\widehat{price_i}) $
,即价格的样本原始数据减去样本预测值。
同时以上三者遵循 SST=SSR+SSM
4、df:自由度
表3:自由度
| 类型 | 计算方法 | 结果 | 注释 |
|---|---|---|---|
| SST | n-1 | 73 | 总样本为74,所以n-1=73 |
| SSE | K | 4 | 模型中回归系数4个加上常数共计5个估计系数,所以(k+1)-1=k=4,其中K表示解释变量个数 |
| SSR | n-k-1 | 69 | 样本量-约束条件=n-(k+1)=n-k-1=74-4-1=69 |
解释:
- (1)Total-总平方和TSS:样本量-动不了的均值=n-1
- (2)Explained-平方和SSE:未知参数个数-动不了的那个均值=(k+1)-1=k
- (3)Residual-残差平方和SSR:样本量-约束条件=n-(k+1)=n-k-1 $SST自由度=SSE的自由度+SSR自由度$
5、R-squared :拟合优度、R^2
计算公式:
$ R^2=\frac{SSM}{SST}=1-\frac{SSE}{SST}=\frac{\sum(\widehat{Y_i}-\overline{Y})^2}{\sum(Y_i-\overline{Y})^2} $
代表了模型中因变量可由自变量解释的方差百分比。换句话说,显示数据与回归模型的拟合程度(拟合优度)
6、 Adj R-squared:调整拟合优度、调整R^2
$ adj.R^2=1-\frac{n-1}{n-k-1}(1-R^2)$
R-squared无法控制变量的增加而导致过度拟合,Adj R-squared则在此基础上,引入了自变量的个数这一因素,以更加准确地评估模型的拟合效果。 在多元线性回归模型中,当自变量的数量增加时,R-squared也会随之增加。但是,当自变量的数量增加时,也容易出现过拟合(overfitting)现象,导致模型的预测能力下降。因此,为了避免过拟合,我们需要使用Adj R-squared对R-squared进行修正。Adj R-squared可以更精确地反映自变量对因变量的解释程度,避免了因自变量数量增加而导致的过拟合问题,是多元线性回归模型中一个比较重要的评估指标。
可以看出,调整的R2随k的增加而减小,(n是样本个数,在调查之后分析时,是固定的),可以识别自变量个数对R2的影响。经验上,一般当k:n大于1:5时,R2会高估实际的拟合优度,这时,宜用调整后的R2来说明方程的拟合优度,也就是自变量对y的解释能力。
7、MS:均方差
计算公式:$ MS=\frac{ss}{df} $
简单理解就是平方和的平均数
8、F:F统计量
$ F=\frac{MS\_model}{MS\_residual} $
F检验的假设检验如下:
- H0:所有的系数为0,即所有解释变量联合对被解释变量影响不显著。
- H1:所有的系数不为0,即所有解释变量联合对被解释变量影响显著。
判断规则F统计量越大越好,对应的P值越小。
9、Prob > F :P值
P值是F统计量对应的概率,,通常有模型在1%、5%、10%水平下拒绝原假设,从而认为自变量对因变量影响的显著水平,也可以说模型在1%、5%、10%水平上显著。P值由F值查表得出。P值指的是假设检验中得到的显著性水平,其英文单词为"p-value"。其中,p表示概率(probability),value则代表一个数值,即显著性水平。
P值是小于1的,如果小于1%、5%、10%,则拒绝原假设,接受备择假设,也可以说模型在1%、5%、10%水平上显著。本文的F统计量为36.10,对应的伴随概率P值为0,说明在1%的显著性水平下,以上4个解释变量对价格的影响是显著的。
表4:p值解释
| p-value | 解释 | 详细解释 |
|---|---|---|
| P < 0.1 | 模型在10%水平上显著 | 解释变量对被解释变量是在1%的显著水平下是显著的 |
| P < 0.05 | 模型在5%水平上显著 | 解释变量对被解释变量是在5%的显著水平下是显著的 |
| P < 0.01 | 模型在1%水平上显著 | 解释变量对被解释变量是在10%的显著水平下是显著的 |
10 、Root MSE:均方误
计算公式: $ Root MSE=\sqrt{MS\_residual} $
衡量模型中的误差项的大小,Root MSE越大,误差越大,Root MSE越小越好。
11、Number of obs:样本量
样本个数对应本文的样本量为74
12、Coef.:系数
回归系数,其中_cons表示常数项
在本文中weight的系数为-0.004,,说明在其他因素不变的情况下,汽车重量每增加1%,将导致汽车价格降低0.004%。同时Foreign的系数为-1.99,说明在其他因素不变的情况下进口车价格比国产车价格低-1.99。(注:由于为示例,所以回归结果并不符合实际。)
13、Std. Err.:标准误
衡量估计系数的波动水平
14、t:t统计量
$ t=\frac{Coef.}{Std.Err.}$
t检验中的字母t来源于英文单词"t-distribution",也就是t分布。T分布是一种概率分布函数,是一类常用于小样本假设检验的概率分布。T分布的形态与自由度有关,当自由度越大时,T分布越趋近于标准正态分布。在t检验中,t值的计算需要用到样本均值、标准差和样本量,然后再根据自由度和置信水平查找t分布表,得到检验的p值,以此来判断是否拒绝零假设。
- H0:,即weight对price的影响不显著。
- H1: ,即weight对price的影响显著。
15、P > | t |:p值
P值,根据t值查表获得
表5:t统计量对应的p值
| P值 | 解释 | 标星 |
|---|---|---|
| P < 0.1 | 系数在10%水平上显著 | 标记* |
| P < 0.05 | 系数在5%水平上显著 | 标记** |
| P < 0.01 | 系数在1%水平上显著 | 标记*** |
16、95% Conf. Interval:95%置信区间
95%置信区间,表示回归系数的取值范围,该范围有效的概率是95%。回归系数的置信区间可以用来估计某个回归系数的真实值有多大的概率落在一个指定的置信区间范围内。回归的标准误差是一个衡量统计可靠性的重要指标,它减小了估计变量的误差,提高了置信区间的准确性。我们可以使用置信区间公式计算置信区间,计算出拟合回归系数的上下限值,即常说的置信区间。拟合系数的置信区间是根据概率统计理论确定的,常常可以用于估计与待定参数有关的信息,预测估计误差,同时也可用于检验统计假设。
参考资料
