【1.4】算法复杂性分析

一、算法的渐进分析

$$f(n)= n^{2} + 100n +log_{10}n + 1000$$

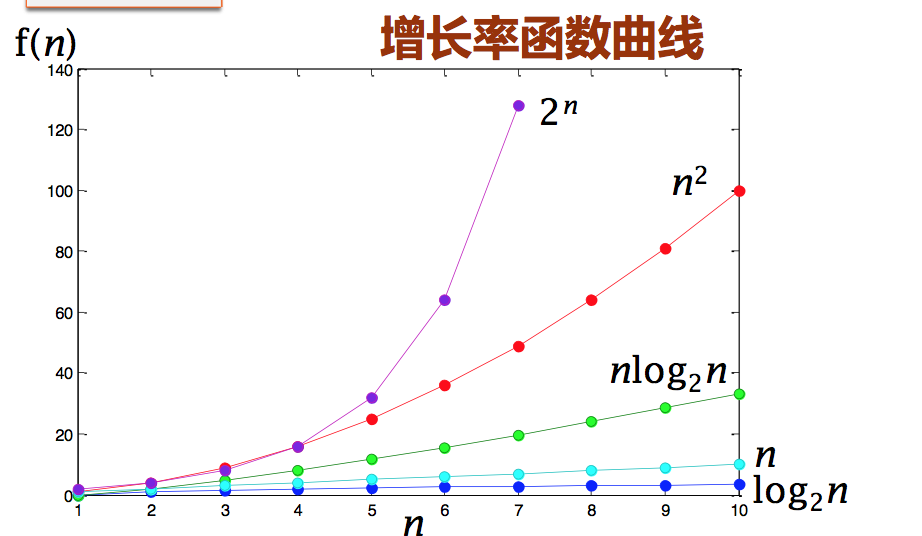
• 数据规模 n 逐步增大时， f(n) 的增长趋势
• 当 n 增大到一定值以后，计算公式中 影响最大的就是 n 的幂次最高的项 – 其他的常数项和低幂次项都可以忽略

1.1 大O表式法

函数 f，g 定义域为自然数，值域非负实数集

定义:如果存在正数 c 和 n0 ，使得对任意的 n 大于等于n0 ， 都有 f(n) 小于等于 cg(n)，

• 称f(n)在集合O(g(n)) 中，简称 f(n) 是 O(g(n)) 的，或 f(n) = O(g(n))

• 大 O 表示法:表达函数增长率上限

• 一个函数增长率的上限可能不止一个

• 当上、下限相同时则可用 Θ 表示法

f(n) = O(g(n)) , 当且仅当

• 存在两个参数 c > 0 ，n0 > 0, 对于所有的 n ≥ n0 ， 都有 f(n) ≤ cg(n)

• iff ∃ c, n0 > 0 s.t. ∀ n ≥ n0 : 0 ≤ f(n) ≤ cg(n)

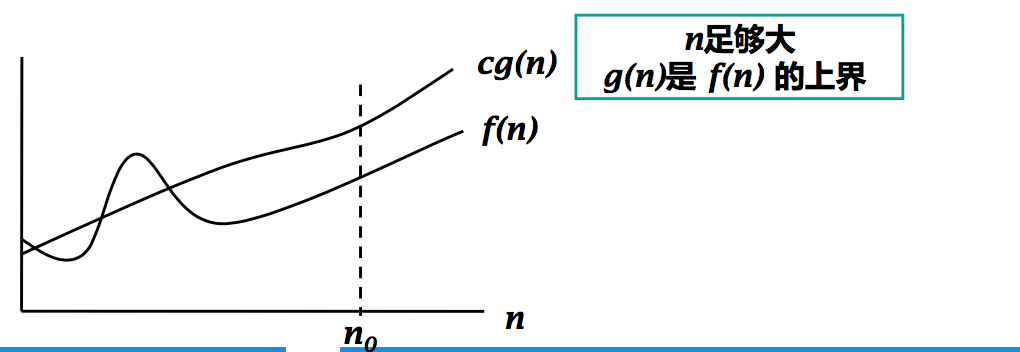
大 O 表示法的单位时间

• 简单布尔或算术运算 *简单 I/O
• 指函数的输入/输出。例如，从数组读数据等操作
• 不包括键盘文件等 I/O
• 函数返回

大 O 表示法的运算法则

1.2 大 Ω 表式法

• 定义 :如果存在正数 c 和 n0，使得对所有的 n ≥ n0， 都有 f(n) ≥ cg(n)， 则称 f(n) 在集合 Ω (g(n)) 中，或简称 f(n) 是 Ω (g(n)) 的， 或 f(n) = Ω (g(n))
• 大 O 表示法和大 Ω 表示法的唯一区别在于不等式的方 向而已
• 采用大 Ω 表示法时， 最好找出在函数增值率的所有下 限中那个最“紧”(即最大)的下限

1.3 大 Θ 表示法

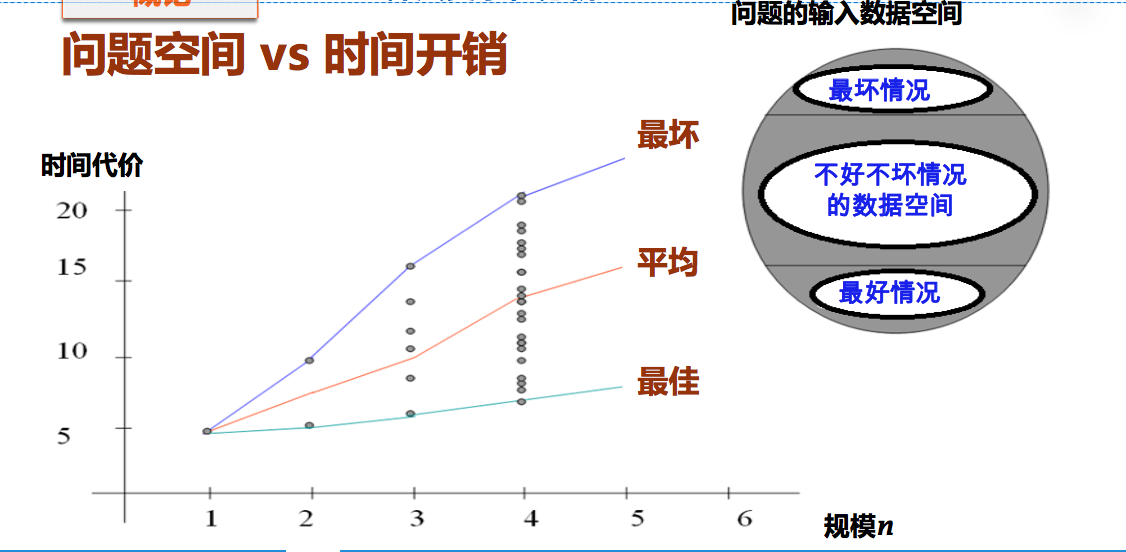
1.4 问题空间 vs 时间开销

二、例子

2.1 顺序找 k 值

• 顺序从一个规模为 n 的一维数组中， 找出一个给定的 K 值
• 最佳情况
• 数组中第 1 个元素就是 K
• 只要检查一个元素
• 最差情况
• K 是数组的最后一个元素
• 检查数组中所有的 n 个元素

顺序找 k 值——平均情况

如果等概率分布

• K 值出现在 n 个位置上概率都是 1/n

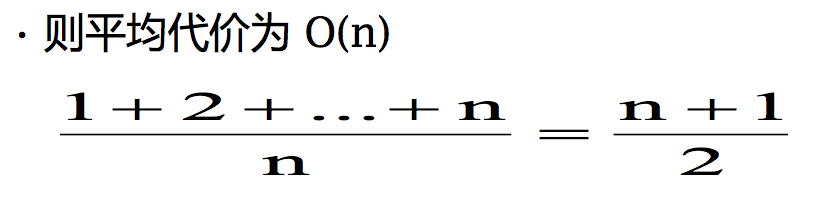
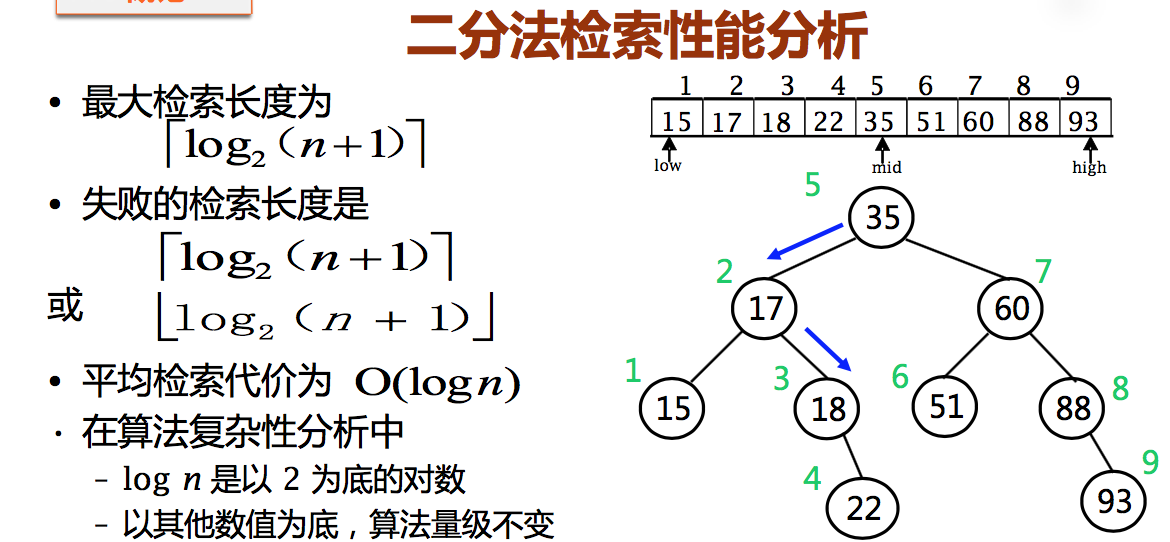
2.2 二分法找 k 值

对于已排序顺序线性表

• 数组中间位置的元素值 kmid
• 如果 kmid = k，那么检索工作就完成了
• 当 kmid > k 时，检索继续在前半部分进行
• 相反地，若 kmid < k，就可以忽略 mid 以前的那部分，检索继续在后半部分进行
• 快速
• kmid = k 结束
• Kmid ≠ k 起码缩小了一半的检索范围

三、讨论

3.1 时间/空间权衡

• 数据结构
• 一定的空间来存储它的每一个数据项
• 一定的时间来执行单个基本操作
• 代价和效益
• 空间和时间的限制
• 软件工程

3.2 数据结构和算法的选择

• 仔细分析所要解决的问题
• 特别是求解问题所涉及的数据类型和数据间逻辑关系 —— 问题抽象、数据抽象
• 数据结构的初步设计往往先于算法设计
• 注意数据结构的可扩展性
• 考虑当输入数据的规模发生改变时， 数据结构是否能够适应求解问题的演变和扩展

3.3 数据结构和算法的选择

• 问题求解的目标?
• 数据结构与算法选择的过程?

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾蛟