【8.6】分配排序和索引排序

• 不需要进行纪录之间两两比较
• 需要事先知道记录序列的一些 具体情况

一、桶式排序

• 事先知道序列中的记录都位于某个小区间 段 [0, m) 内
• 将具有相同值的记录都分配到同一个桶中 ，然后依次按照编号从桶中取出记录，组 成一个有序序列

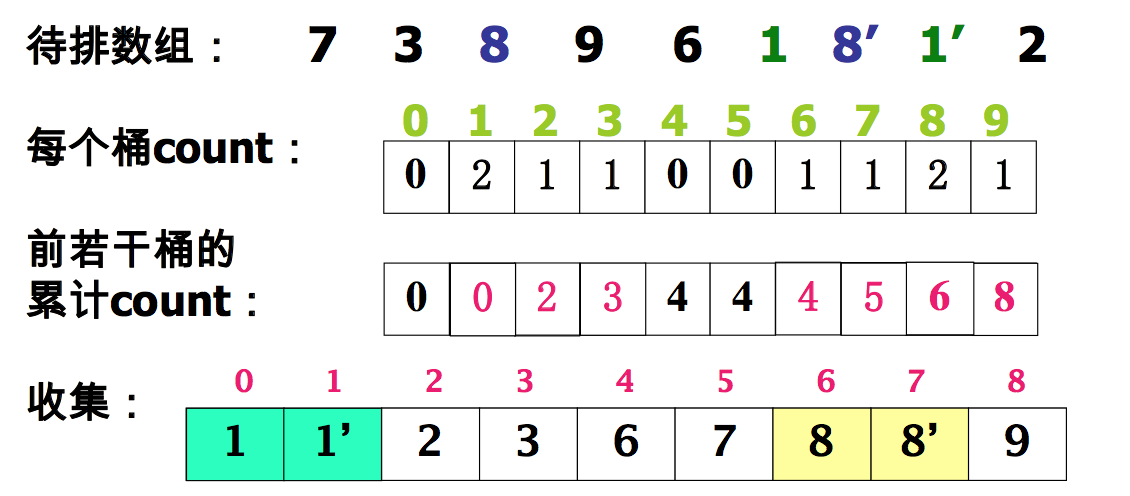
桶式排序算法：

算法分析：

• 数组长度为 n, 所有记录区间 [0, m) 上

• 时间代价:

• 统计计数:Θ(n+m) ， 输出有序序列时循环 n 次

• 总的时间代价为 Θ(m+n)

• 适用于 m 相对于 n 很小的情况

• 空间代价:

• m 个计数器，长度为 n 的临时数组，Θ(m+n)

• 稳定

思考

1. 桶排事先知道序列中的记录都位于某个小区间 段 [0，m) 内。m 多大合适?超过这个范围怎 么办?

2. 桶排中，count 数组的作用是什么?为什么桶 排要从后往前收集?

二、 基数排序

• 桶式排序只适合 m 很小的情况

• 基数排序: 当 m 很大时，可以将一个记录的值即排序码拆分为多个部分来进行比较

• 假设长度为 n 的序列 R = { r0，r1，…，r_n-1 } 记录的排序码 K 包含 d 个子排序码 K = ( k_d-1，k_d-2，…，k₁，k₀ )

• R 对排序码有序，即对于任意 两个记录Ri，Rj (0≤i<j≤n-1)，都满足 (k_{i ,d-1}，k _{i ,d-2}， …，k _{i ,1}，k_i,0 ) ≤ (k _{j ,d-1}，k _{j, d-2}，…，k _j,1，k _j,0 )

例子:

例如:对 0 到 9999 之间的整数进行排序

• 将四位数看作是由四个排序码决定，即千、百 、十、个位，其中千位为最高排序码，个位为 最低排序码。基数 r=10。
• 可以按千、百、十、个位数字依次进行4次桶 式排序
• 4趟分配排序后，整个序列就排好序了

高位优先法

• MSD，Most Significant Digit first
• 先处理高位 kd-1 将序列分到若干桶中
• 然后再对每个桶处理次高位 kd-2 ，分成更小的桶
• 依次重复，直到对 k0 排序后，分成最小的桶， 每个桶内含有相同排序码 (kd-1，…，k1，k0 )
• 最后将所有的桶中的数据依次连接在一起， 成为一个有序序列
• 这是一个 分、分、…、分、收 的过程

低位优先法

• LSD，Least Significant Digit first
• 从最低位 k0 开始排序
• 对于排好的序列再用次低位 k1 排序;
• 依次重复，直至对最高位 kd-1 排好序后， 整个序列成为有序的
• 分、收;分、收;…;分、收的过程
• 比较简单，计算机常用

基数排序的实现

• 主要讨论 LSD

• 基于顺序存储

• 基于链式存储

• 原始输入数组 R 的长度为 n，基数为 r，排序 码个数为 d

基于顺序存储的基数排序:

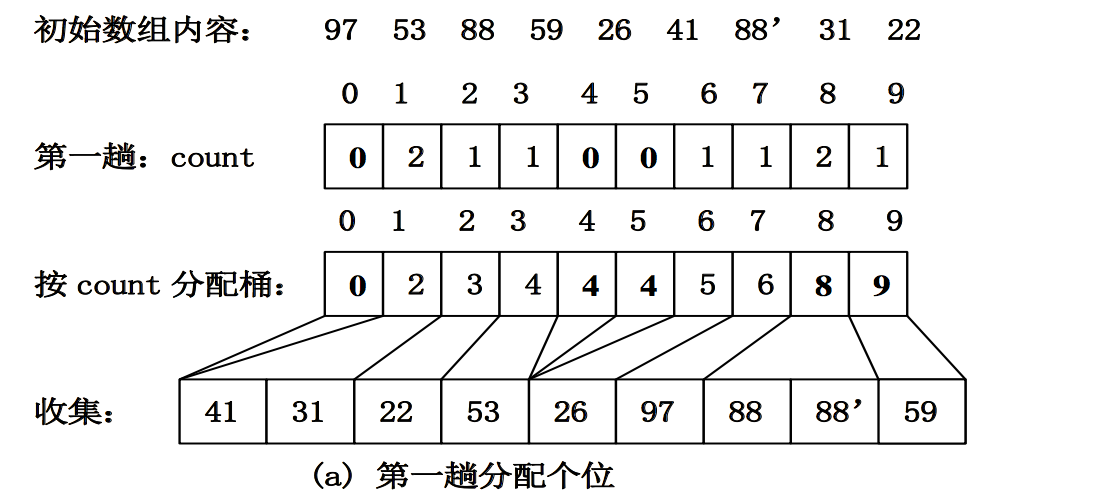
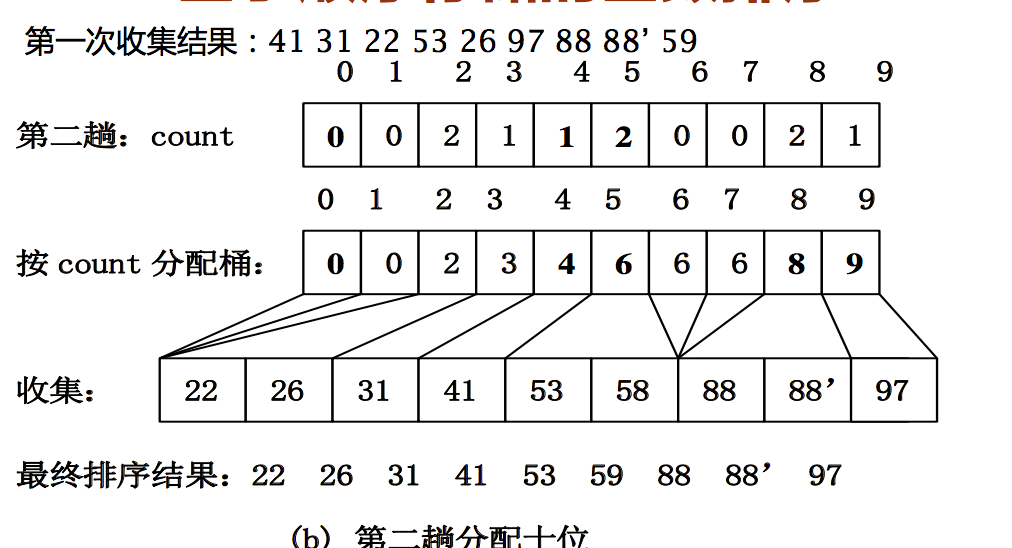
基于数组的基数排序

顺序基数排序代价分析

• 空间代价:

• 临时数组, n

• r 个计数器

• 总空间代价 Θ(n+r)

• 时间代价

• 桶式排序:Θ(n+r)

• d 次桶式排序

• Θ(d·(n+r))

思考:排序该排什么?

2.2 基于静态链的基数排序

• 将分配出来的子序列存放在 r 个 (静 态链组织的) 队列中
• 链式存储避免了空间浪费情况

静态队列定义：

基于静态链的基数排序：

链式基数排序算法代价分析：

• 空间代价

• n 个记录空间

• r 个子序列的头尾指针

• Θ(n + r)

• 时间代价

• 不需要移动记录本身，只需要修改记录的 next 指针

• Θ(d·(n+r))

基数排序效率：

• 时间代价为Θ(d·n)， 实际上还是 Θ(nlog n)
• 没有重复关键码的情况，需要 n 个不同的编 码来表示它们
• 也就是说，d >= logrn，即在 Ω(log n) 中

思考:排序该排什么?

1. 桶排事先知道序列中的记录都位于某个小区间 段 [0，m) 内。m 多大合适?超过这个范围怎 么办?
2. 桶排中，count 数组的作用是什么?为什么桶 排要从后往前收集?
3. 顺序和链式基数排序的优劣?
4. 链式基数排序的结果整理?

有头结点的单链表的插入算法

链式基数排序的结果

三、索引地址排序

基数排序的结果地址索引表示

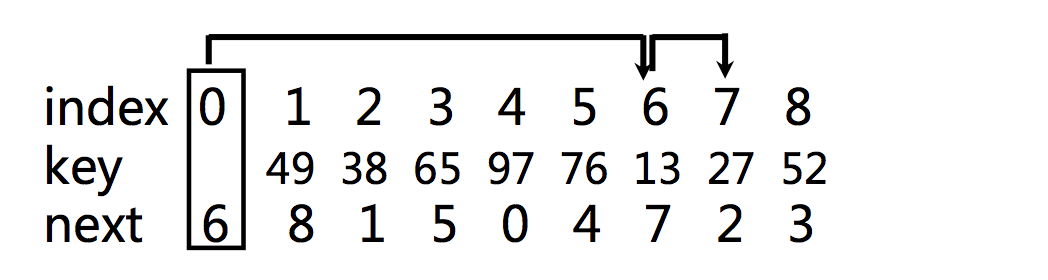
• 有头结点的单链表的插入算法
• 链式基数排序的结果

线性时间整理静态链表

索引数组

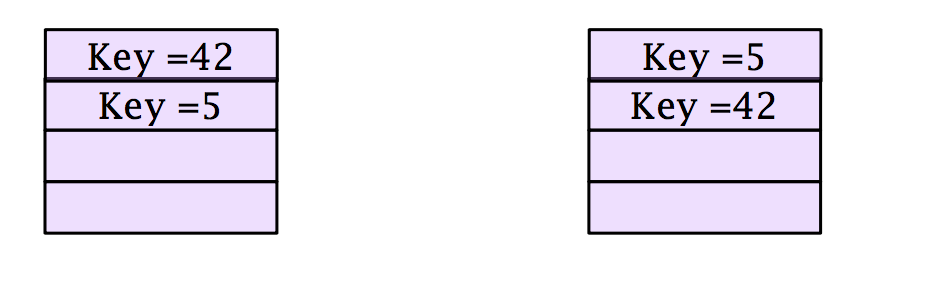
数据域很大，交换记录的代价比较高

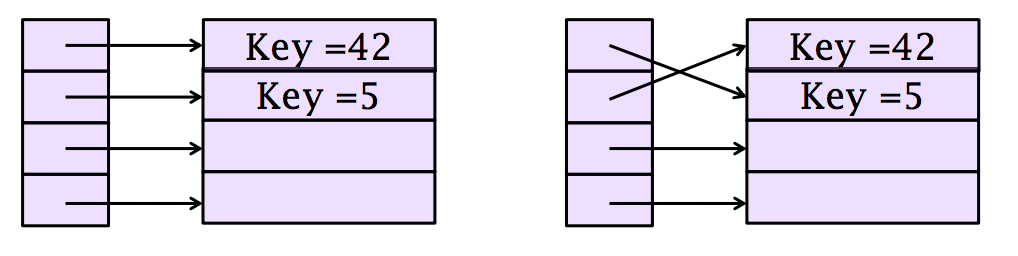
交换指针，减少交换记录的次数

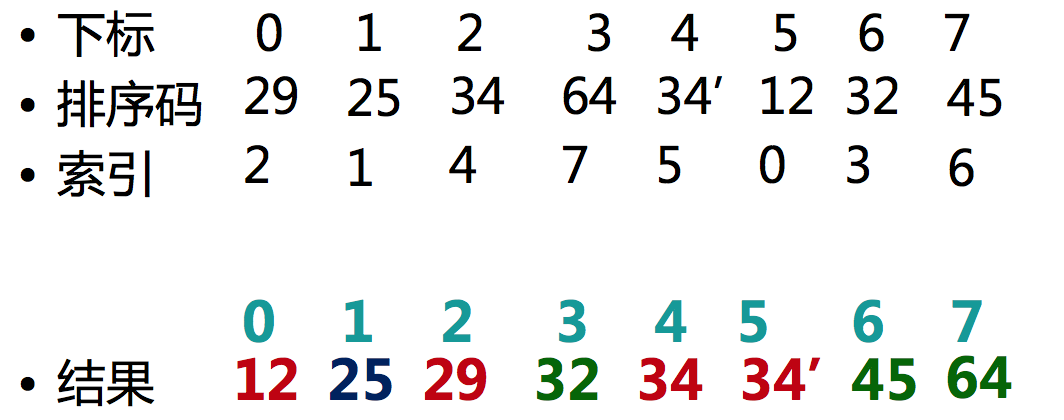
索引结果

• 结果下标 IndexArray[i] 存放的是 Array[i] 中应该摆放的数据位置。
• 整理后 Array[i] 对应原数组中 Array[IndexArray[i]]

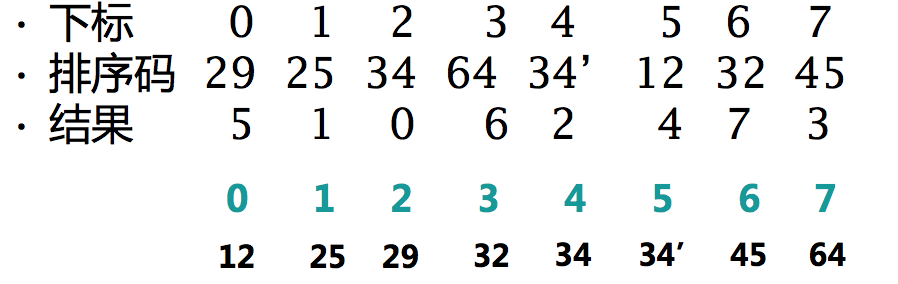
索引排序的适用性

• 一般的排序方法都可以

• 那些赋值(或交换)都换成对index 数组的赋值(或交换)

• 举例:插入排序

插入排序的索引地址排序版本

对索引数组的顺链整理

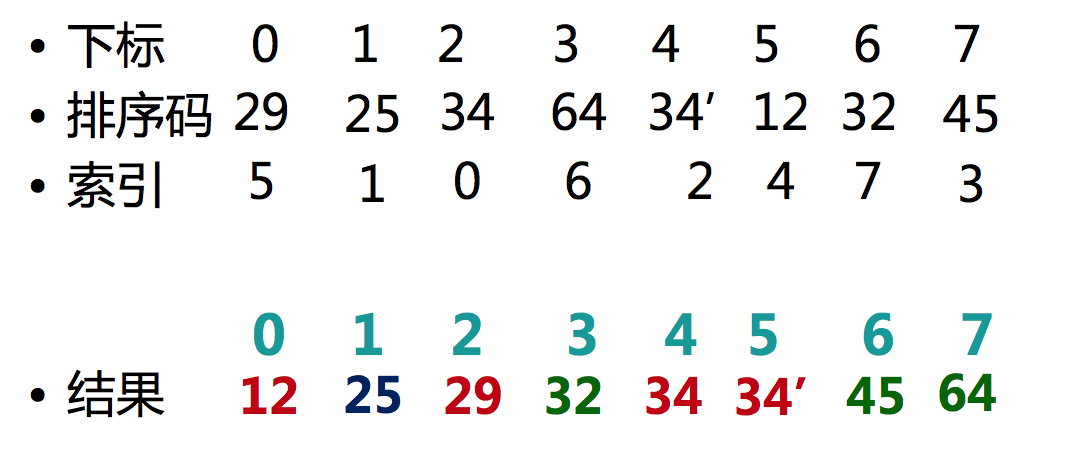
插入排序的索引地址排序版本(续)

第二种索引方法

• 结果下标 IndexArray[i] 存放的是 Array[i] 中数据应该待的位置。
• 排好序的 Array[IndexArray[i]] 对应原数组 中 Array[i]

对第二种索引的顺链整理

思考

1. 证明地址排序整理方案的时间代价为 𝜃(𝑛)
2. 修改快速排序，得到第一种索引结果
3. 采用 Rank 排序得到第二种索引的方法
4. 对静态链的基数排序结果进行简单变换得到第二种索引的方法

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾