【7.1】图的定义和术语

G= (V，E) 表示

• V 是顶点 (vertex) 集合

• E 是边 (edge) 的集合

• 完全图 (complete graph)

• 稀疏图 (sparse graph)

• 稀疏度(稀疏因子)

• 边条数小于完全图的5%

• 密集图 (dense graph)

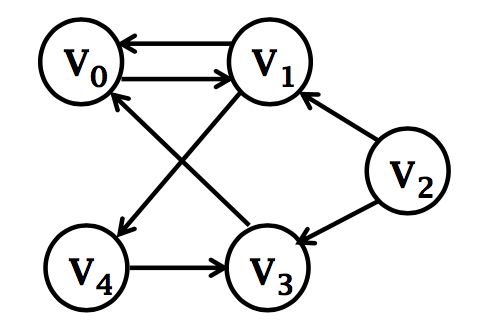
无向图

• 边涉及顶点的偶对无序
• 实际上是双通

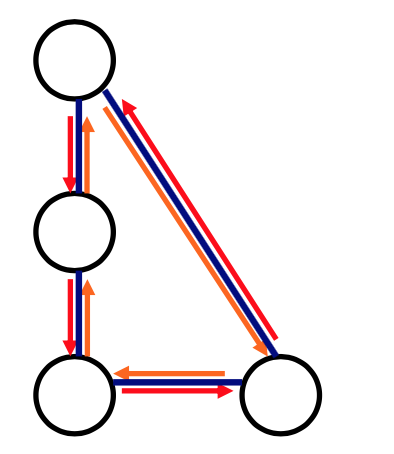
有向图

• 有向图 (directed graph 或 digraph)
• 边涉及顶点的偶对是 有序 的

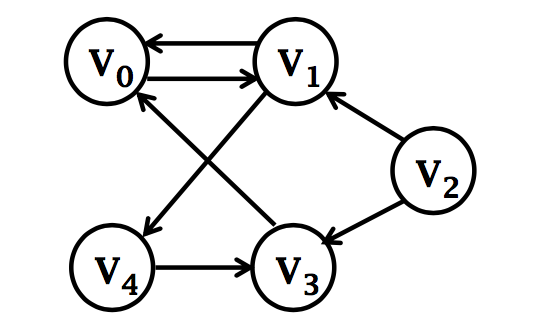
标号图

标号图 (labeled graph)

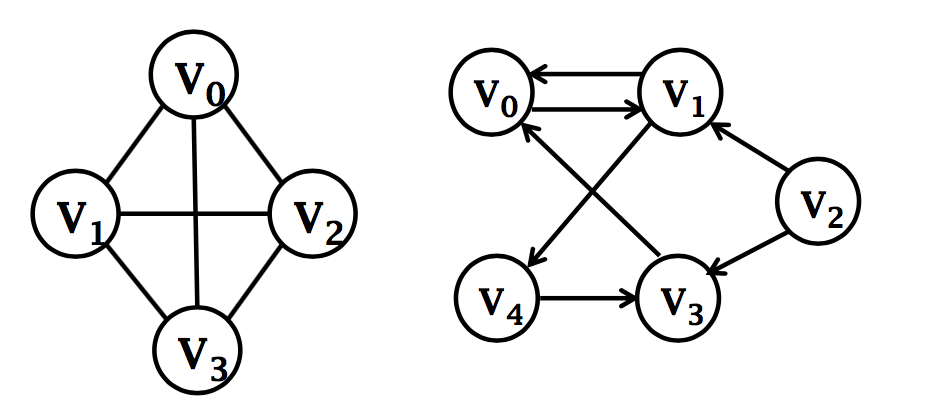
带权图

带权图 (weighted graph)

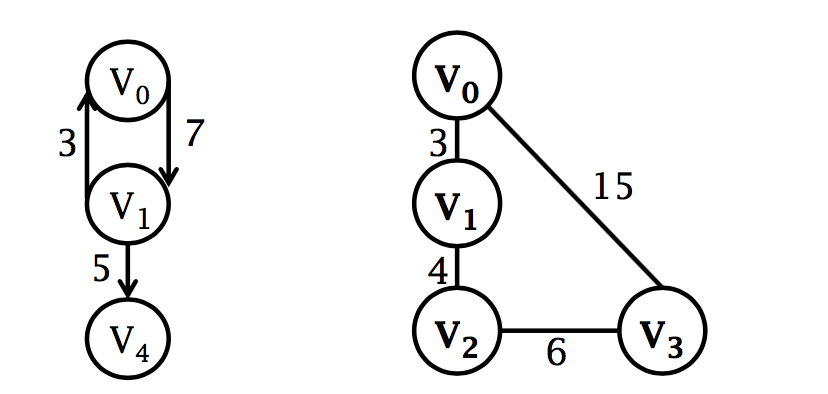
顶点的度 (degree)

与该顶点相关联的边的数目：

• 入度(indegree)
• 出度 ( out degree )

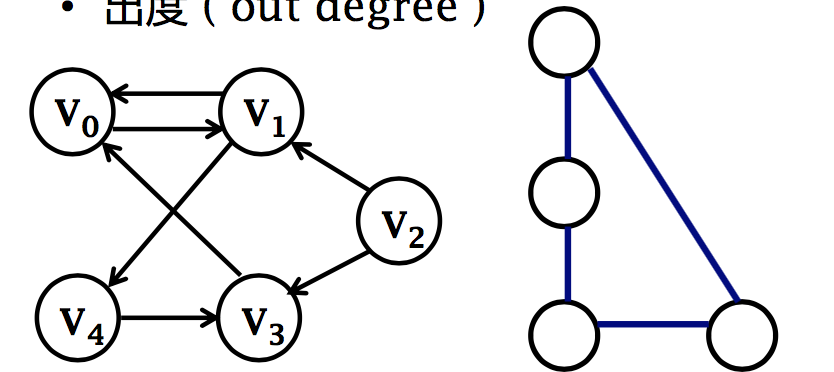
子图 (subgraph)

图G= ( V，E )，G’= ( V’，E’)中，若 V’≤V， E’≤E，并且 E’中的边所关联的顶点都在 V’ 中，则称图G’是图G的 子图

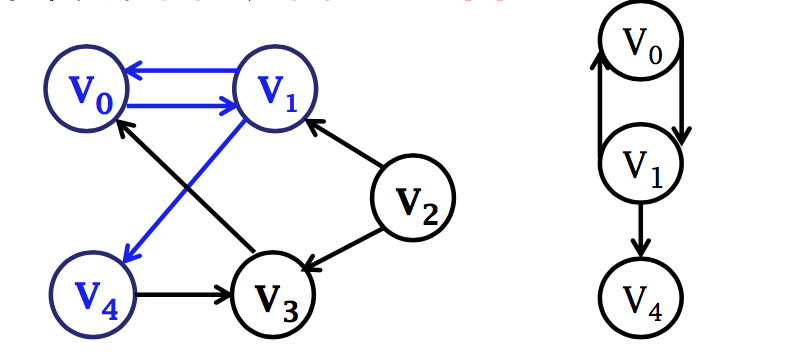
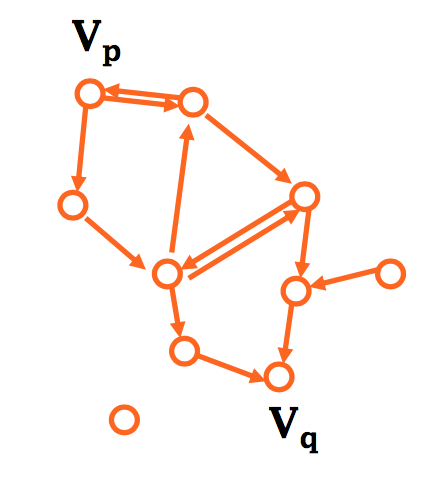
路径 (path)

• 从顶点Vp到顶点Vq的路径
• 顶点序列Vp，Vi1，Vi2，…， Vin，Vq，使得 (Vp，Vi1) ， (Vi1，Vi2) ，…， (Vin，Vq) (若对有向图，则使得<Vp， Vi1>，<Vi1，Vi2> ，…， <Vin，Vq>) 都在 E 中
• 简单路径 (simple path)
• 路径长度 (length)

回路 (cycle，也称为环)

• 简单回路 (simple cycle)
• 无环图 (acyclic graph)
• 有向无环图 (directed acyclic graph，简写为DAG)

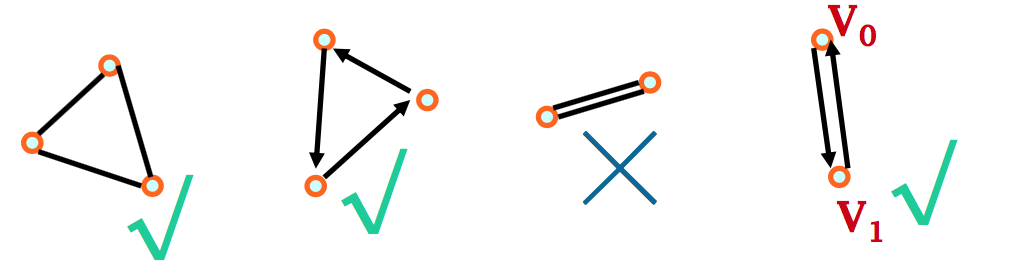
无向图中，如果两个结点之间有平行边，容易 让人误看作“环”)。无向图路径长度大于等于 3

有向图两条边可以构成环，例如<V0，V1>和<V1，V0> 构成环

有根图

• 一个有向图中，若存在一个顶点 V0， 从此顶点有路径可以到达图中其它所 有顶点，则称此有向图为有根的图， V0 称作图的根
• 树、森林

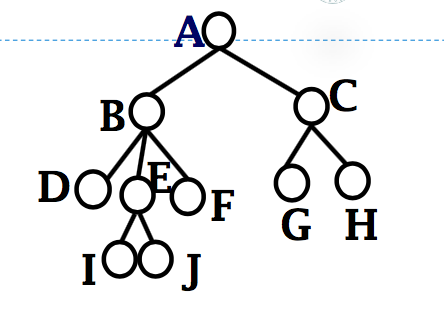
连通图

对无向图 G= (V，E) 而言，如果从 V1 到 V2 有一 条路径 (从 V2 到 V1 也一定有一条路径) ，则称 V1 和V2 是连通的 (connected)

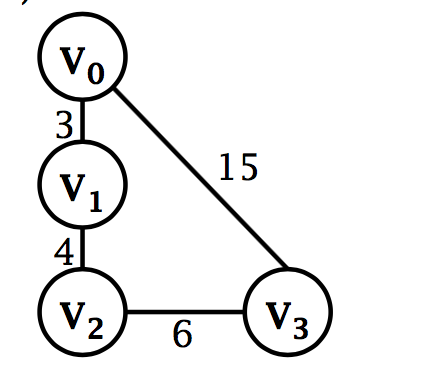
无向图连通分支(连通分量)

无向图的最大连通子图

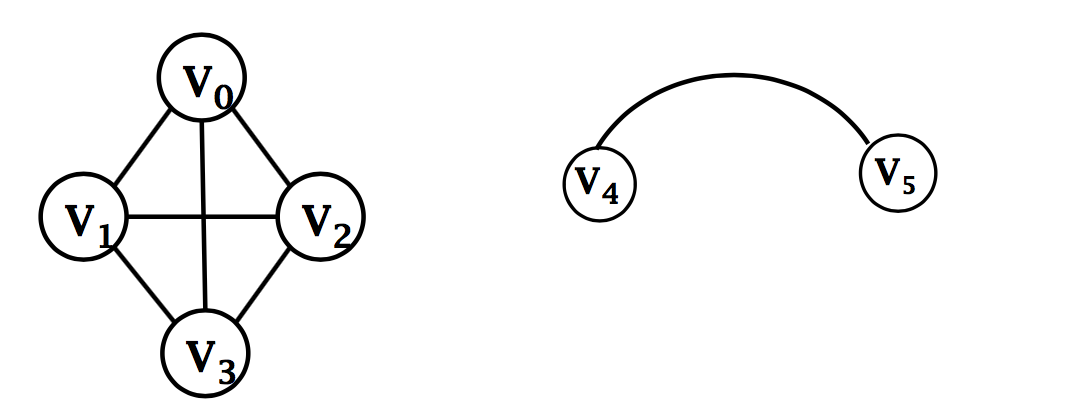
有向图的强连通分量

• 有向图 G (V,E)，如果两个顶点 vi,vj 间 (vi$<>$vj) 有一条 从 vi 到 vj 的有向路径，同时还有一条从 vj 到 vi 的有 向路径，则称两个顶点 强连通
• 非强连通图有向图的极大强连通子图，称为 强连通分量 (strongly connected components)。

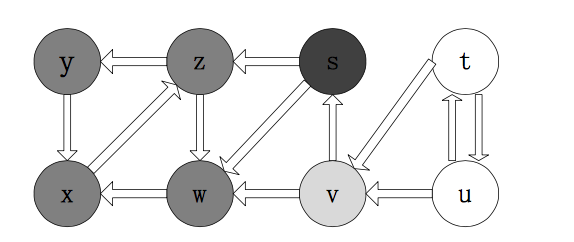
网络

带权的连通图

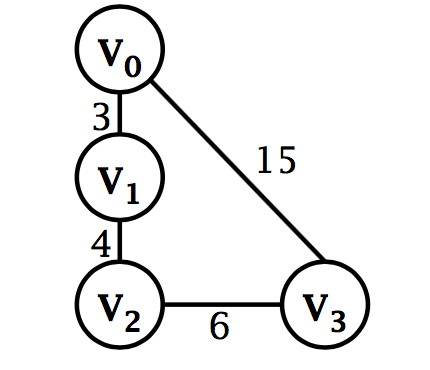
思考

为何不允许一条边的起点与终点都是同一 个顶点?

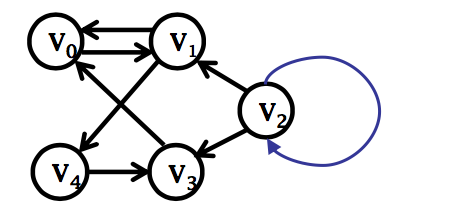
是否存在多条起点与终点都相同的边?

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾