【5.5】堆与优先队列
一、堆的定义及其实现
最小堆:最小堆是一个关键码序列
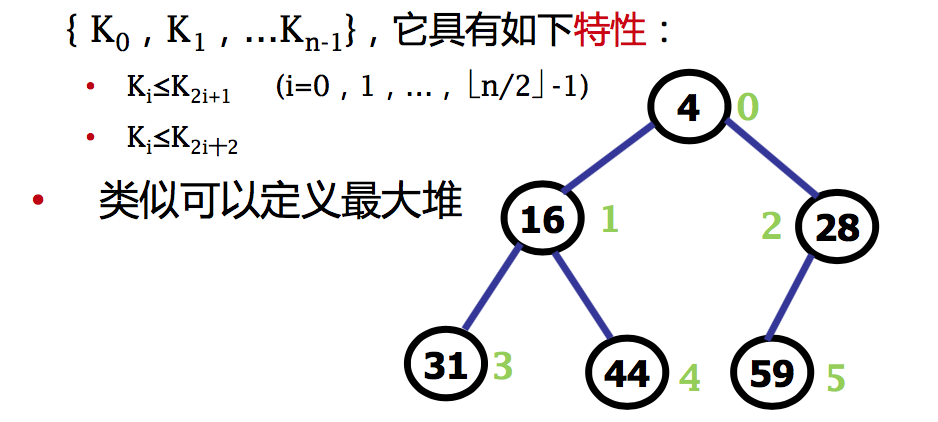
堆的性质
- 完全二叉树的层次序列,可以用数组表示
- 堆中储存的数是局部有序的,堆不唯一
- 结点的值与其孩子的值之间存在限制
- 任何一个结点与其兄弟之间都没有直接的限制
- 从逻辑角度看,堆实际上是一种树形结构
堆的类定义

对最小堆用筛选法 SiftDown 调整
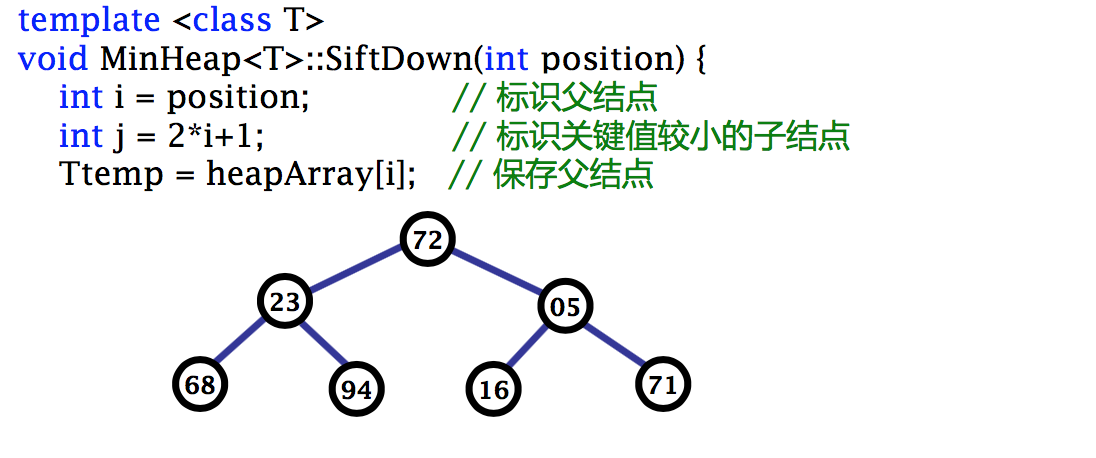

对最小堆用筛选法 SiftUp 向上调整

二、建最小堆过程
- 首先,将 n 个关键码放到一维数组中
- 整体不是最小堆
- 所有叶结点子树本身是堆 (当i≥【n/2】时,以关键码 Ki 为根的子树已经是堆)
- 从倒数第二层,i= [n/2]- 1 开始 从右至左依次调整
- 直到整个过程到达树根
- 整棵完全二叉树就成为一个堆
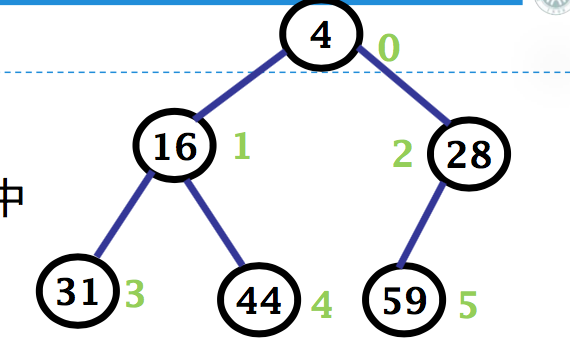
建最小堆过程示意图:
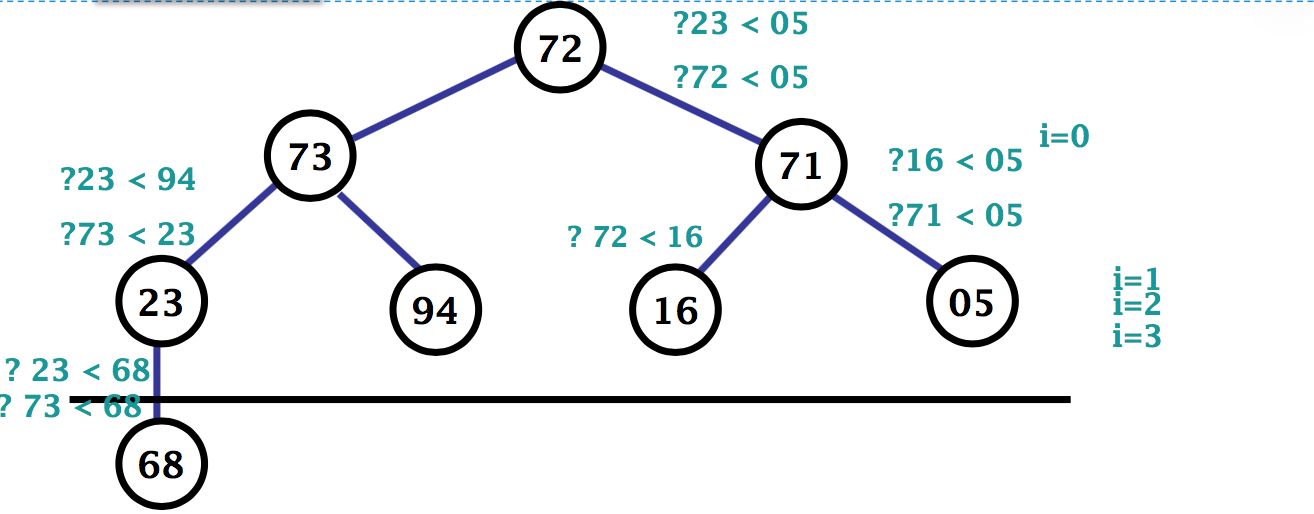
从第一个分支结点 heapArray[CurrentSize/2-1] 开始,自底向上逐步把以子树调整成堆

最小堆插入新元素

最小堆删除元素操作

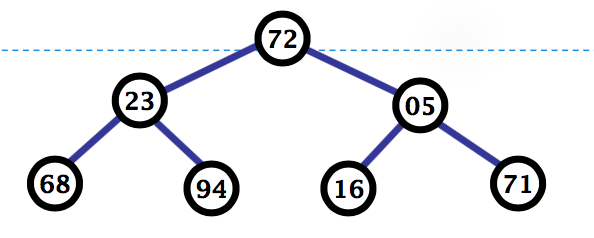
删除68

删除16

建堆效率分析

最小堆操作效率
建堆算法时间代价为 O(n)
堆有logn层深:
- 插入结点、删除普通元素和删除最小元素的平均时间代价和最差时间代价都是 O(log n)
三、优先队列
- 堆可以用于实现优先队列
- 优先队列
- 根据需要释放具有最小(大)值的对象
- 最大树、 左高树HBLT、WBLT、MaxWBLT
- 改变已存储于优先队列中对象的优先权
- 辅助数据结构帮助找到对象
思考
- 在向下筛选SiftDown操作时,若一旦发现 逆序对,就交换会怎么样?
- 能否在一个数据结构中同时维护最大值和 最小值?(提示:最大最小堆)
。。。。
参考资料
北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾
这里是一个广告位,,感兴趣的都可以发邮件聊聊:tiehan@sina.cn
![]() 个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn
个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn

