【5.6】Huffman树及其应用

一、Huffman树定义

1.1 等长编码

• 计算机二进制编码
• ASCII 码
• 中文编码
• 等长编码
• 假设所有编码都等长，表示 n 个不同的字符需要 log2 n位
• 字符的使用频率相等
• 空间效率

1.2 数据压缩和不等长编码

• 频率不等的字符:

• 可以利用字符的出现频率来编码
• 经常出现的字符的编码较短，不常出现的字符编码较长
• 数据压缩既能节省磁盘空间，又能提高运算速度(外存时空权衡的规则)

1.3 前缀编码

• 任何一个字符的编码都不是另外一个 字符编码的前缀
• 这种前缀特性保证了代码串被反编码 时，不会有多种可能。例如
• 右图是一种前缀编码，对于 “000110” ，可以翻译出唯一的字符串“EEEL”。
• 若编码为Z(00), K(01), F(11), C(0), U(1), D(10), L(110), E(010) 。 则 对 应 : ”ZKD”,”CCCUUC”等多种可能

1.4 Huffman树与前缀编码

• Huffman编码将代码与字符相联系
• 不等长编码
• 代码长度取决于对应字符的相对使用 频率或“权”

二、建立Huffman编码树

对于n个字符K0，K1，…，Kn-1，它们的使用频率分别 为w0, w1，…，wn-1，给出它们的前缀编码，使得总 编码效率最高

给出一个具有n个外部结点的扩充二叉树：

• 该二叉树每个外部结点 Ki 有一个权 wi 外部路径长度为 𝑙𝑖
• 这个扩充二叉树的叶结点带权外部路径长度总和

$$ \sum_{i=0}^{n-1} w_{i} l_{i}$$

• 权越大的叶结点离根越近

过程：

• 首先，按照“权”(例如频率)将字符排为一列
• 接着，拿走前两个字符(“权”最小的两个字符)
• 再将它们标记为Huffman树的树叶，将这两个树叶标为一个分支结点的两个孩子，而该结点的权即为两树叶的权之和
• 将所得“权”放回序列，使“权”的顺序保持
• 重复上述步骤直至序列处理完毕

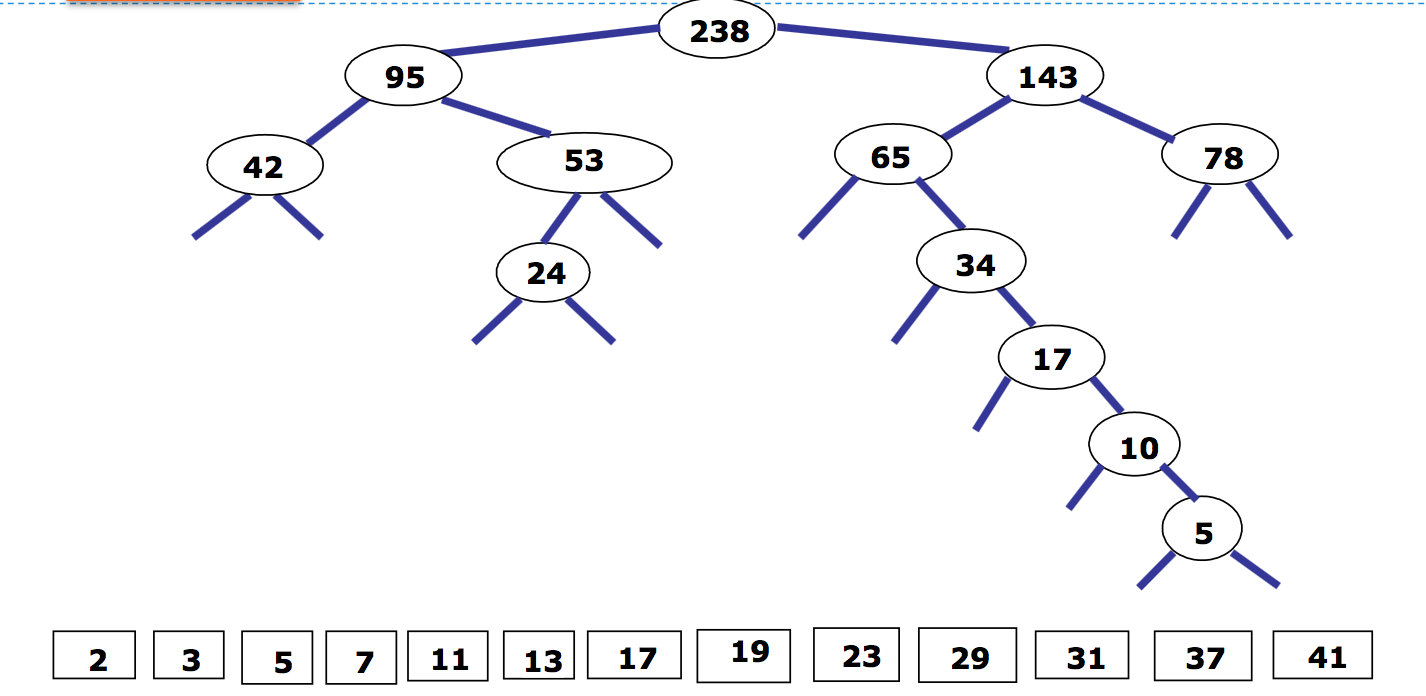
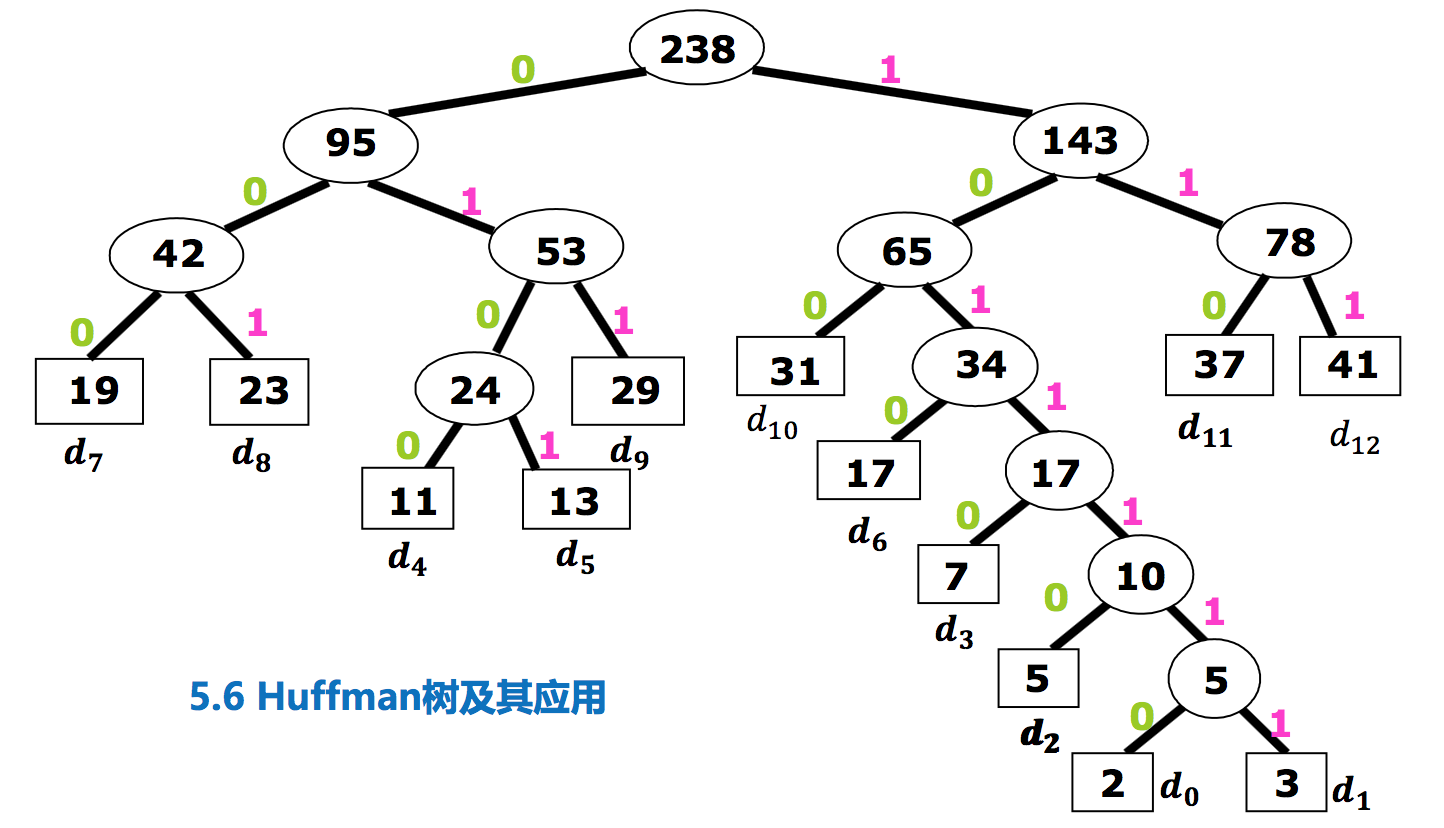
频率越大其编码越短：

各字符的二进制编码为:

译码: 从左至右逐位判别代码串， 直至确定一个字符

与编码过程相逆：

• 从树的根结点开始
• “0”下降到左分支
• “1”下降到右分支
• 到达一个树叶结点，对应的字符就是文本信息的字符

连续译码：

• 译出了一个字符，再回到树根，从二进制位串中的 下一位开始继续译码

Huffman树类

Huffman树的构造

Huffman方法的正确性证明

• 是否前缀编码?
• 贪心法的一个例子
• Huffman树建立的每一步，“权”最小的 两个子树被结合为一新子树
• 是否最优解?

三、Huffman性质

引理： 含有两个以上结点的一棵 Huffman 树 中，字符使用频率最小的两个字符是兄 弟结点，而且其深度不比树中其他任何 叶结点浅

证明：

• 记使用频率最低的两个字符为 y1 和 y2
• 假设 x1, x2 是最深的结点
• y1和y2的父结点Y一定会有比X更大的“权”
• 否则，会选择 Y 而不是 X 作为结点V的子结点
• 然而，由于 y1 和 y2 是频率最小的字符， 这种情况不可能发生

定理:

• 对于给定的一组字符，函数HuffmanTree 实现了“最小外部路径权重”

证明:

• 对字符个数n作归纳进行证明

初始情况:

• 令n = 2, Huffman树一定有最小外部路径权重
• 只可能有成镜面对称的两种树
• 两种树的叶结点加权路径长度相等

归纳假设:

假设有n-1个叶结点的由函数HuffmanTree产生的 Huffman树有最小外部路径权重

归纳步骤:

Huffman树编码效率

• 估计Huffman编码所节省的空间
• 平均每个字符的代码长度等于每个代码的长度 ci乘以其出现的概率 pi ，即:
• c0p0 + c1p1 + … + cn-1pn-1 或 (c0f0 + c1f1 + … + cn-1fn-1) / fT

这里fi为第i个字符的出现频率，而fT为所有字符出现的 总次数

四、Huffman树的应用

• Huffman编码适合于 字符 频率不等，差别较大的情况
• 数据通信的二进制编码
• 不同的频率分布，会有不同的压缩比率
• 大多数的商业压缩程序都是采用几种编码方式以 应付各种类型的文件 （Zip 压缩就是 LZ77 与 Huffman 结合）
• 归并法外排序，合并顺串

思考

• 当外部的数目不能构成满b叉 Huffman 树时，需附加多少个 权为 0的“虚”结点?请推导

• R 个外部结点，b叉树

• 若(r-1)% (b-1)==0，则不需要加“虚”结点

• 否则需要附加 b -(r-1)% (b-1) - 1个“虚” 结 点,即第一次选取(r-1)% (b-1) + 1个非0权值

• 试调研常见压缩软件所使用的编码方式

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾