【12.1】高级数据结构-- 多维数组
一、基本概念
- 数组 (Array) 是数量和元素类型固定的 有序序列
- 静态数组必须在定义它的时候指定其大小 和类型
- 动态数组可以在程序运行才分配内存空间
- 多维数组 (Multi-array) 是向量的扩充
- 向量的向量就组成了多维数组
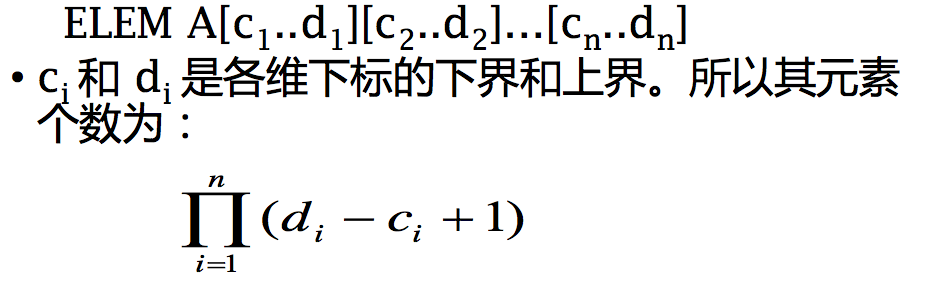
二、数组的空间结构

三、数组的存储
- 内存是一维的,所以数组的存储也只能是一维的
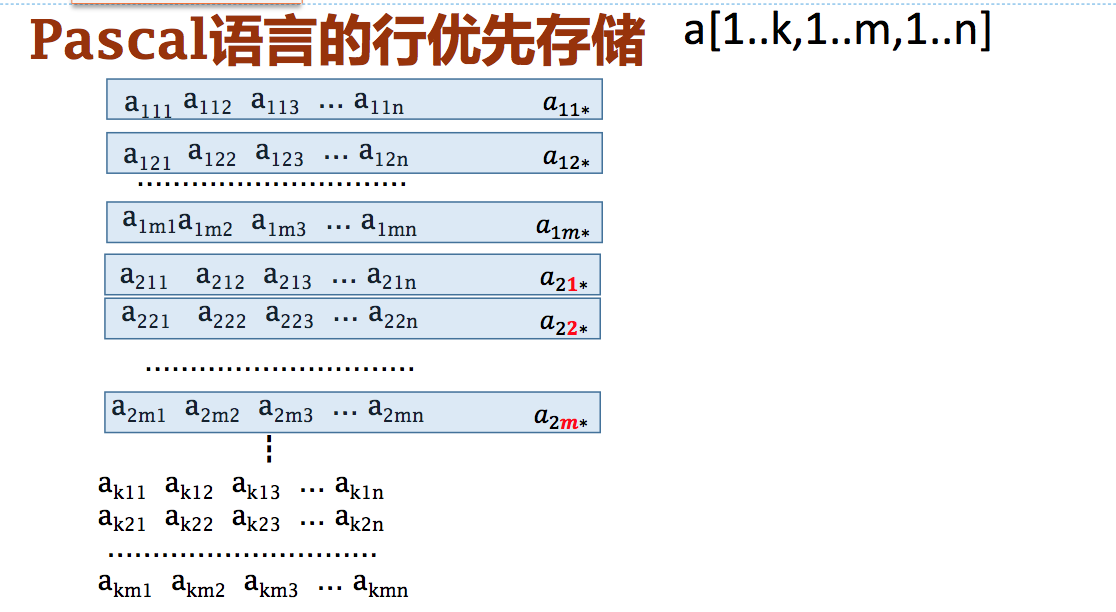
- 以行为主序 (也称为“行优先”)
- 以列为主序 (也称为“列优先”)
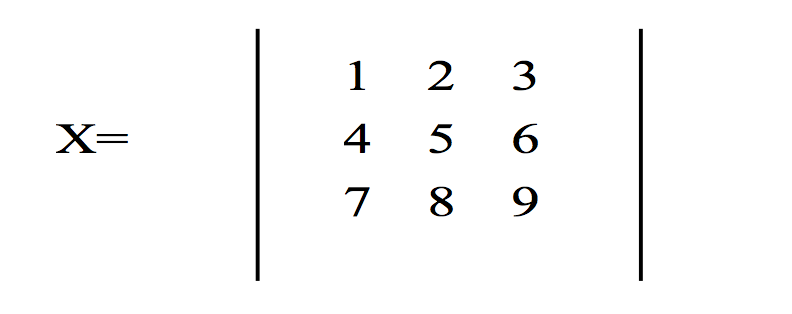
四、数组的声明


五、用数组表示特殊矩阵
- 三角矩阵:上三角、下三角
- 对称矩阵
- 对角矩阵
- 稀疏矩阵
5.1 下三角矩阵图例

5.2 对称矩阵

5.3 对角矩阵
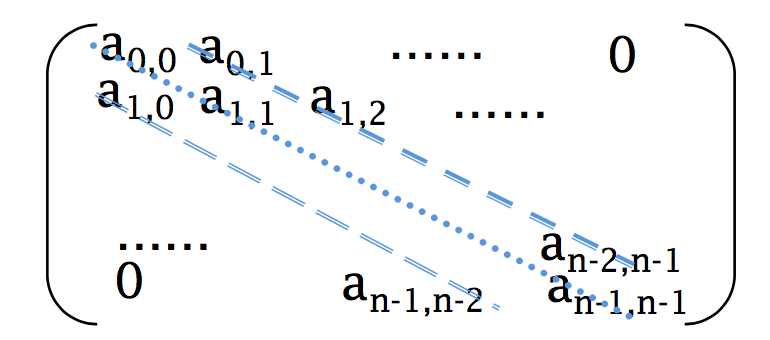
- 对角矩阵是指:所有的非零元素都集中在主对角线及以 它为中心的其他对角线上。
- 如果 |i-j| > 1,那么数组元素 a[i][j] = 0。
- 下面是一个三对角矩阵:
5.4 稀疏矩阵
稀疏矩阵中的非零元素非常少,而且分布也不规律

六、稀疏矩阵
稀疏因子:
- 在 m×n 的矩阵中,有 t 个非零元素,则稀疏因子 为: δ = t/(m*n)
- 当这个值小于0.05时,可以认为是稀疏矩阵
三元组 (i, j, aij) :输入/输出常用
- i 是该元素的行号
- j 是该元素的列号
- aij 是该元素的值
6.1 稀疏矩阵的十字链表
十字链表有两组链表组成:
- 行和列的指针序列
- 每个结点都包含两个指针:同一行的后继,同一列的后继
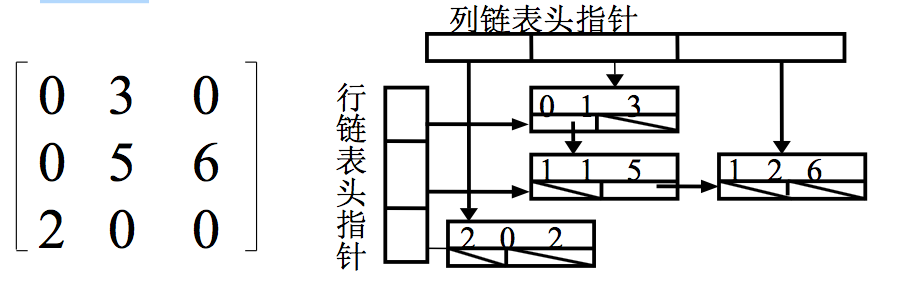
6.2 经典矩阵乘法
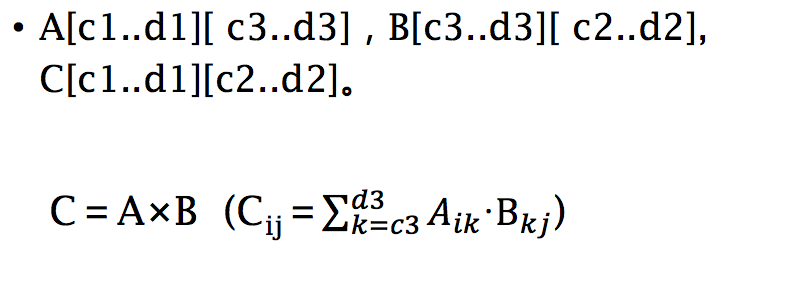
经典矩阵乘法时间代价
- p=d1-c1+1,m=d3-c3+1,n=d2-c2+1;
- A 为 p×m 的矩阵,B 为 m×n 的矩阵,乘得的结果 C 为 p×n 的矩阵
- 经典矩阵乘法所需要的时间代价为 O (p×m×n)

6.3 稀疏矩阵乘法
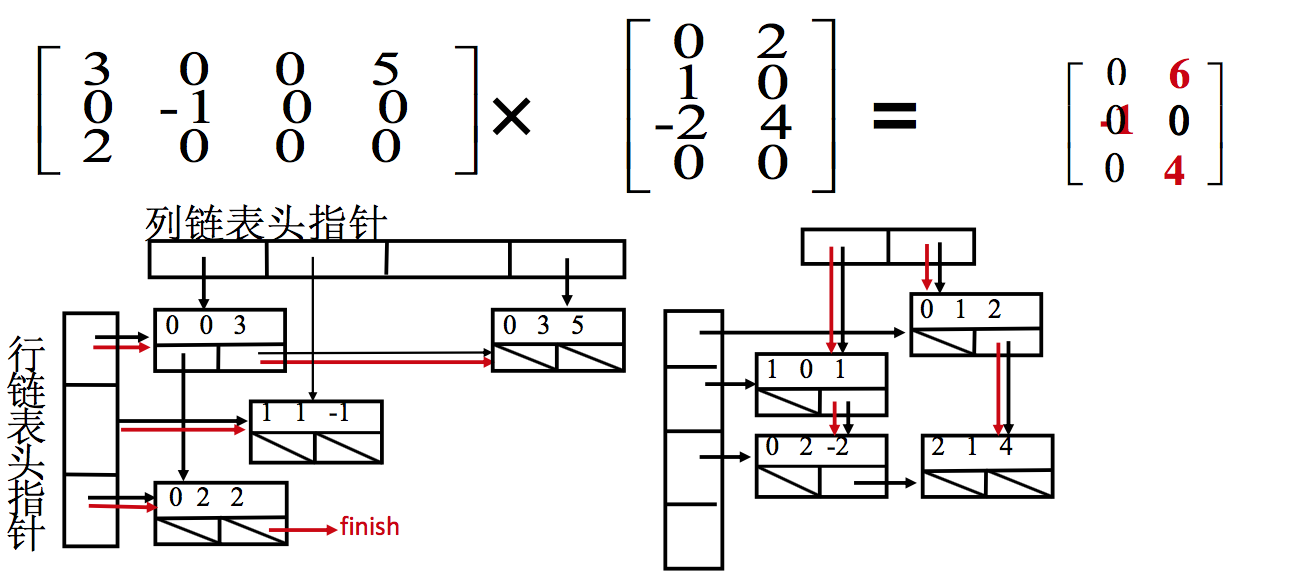
稀疏矩阵乘法时间代价
- A为 p×m 的矩阵,B 为 m×n 的矩阵,乘得的结果 C 为 p×n 的矩阵
- 若矩阵 A 中行向量的非零元素个数最多为 ta
- 矩阵 B 中列向量的非零元素个数最多为 tb
- 总执行时间降低为 O ( (ta+tb) × p × n)
- 经典矩阵乘法所需要的时间代价为 O (p × m × n)
6.4 稀疏矩阵的应用
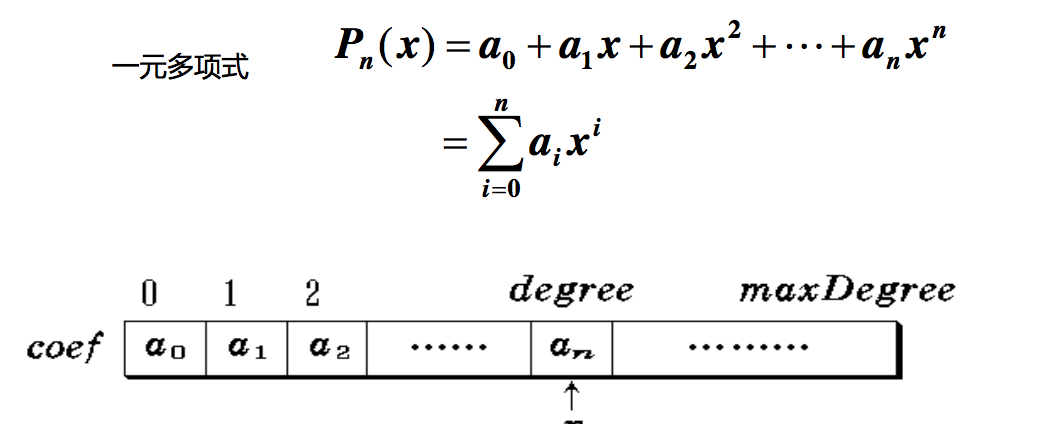
6.5 思考
多元多项式如何使用矩阵表示?如何 使用稀疏矩阵进行存储?
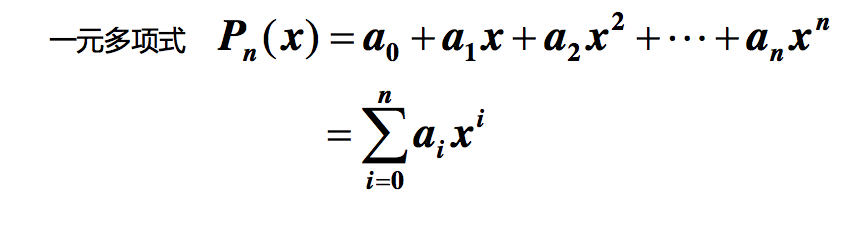
如何用十字链表结构求解数独(sudoku) 问题?
参考资料
北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾
这里是一个广告位,,感兴趣的都可以发邮件聊聊:tiehan@sina.cn
![]() 个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn
个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn

