【4.3】字符串的模式匹配
字符串的模式匹配:
- 模式匹配 (pattern matching)
- 一个目标对象 T(字符串)
- (pattern)P(字符串)
- 在目标 T 中寻找一个给定的模式P的过程
- 应用
- 文本编辑时的特定词、句的查找 UNIX/Linux: sed, awk, grep – DNA 信息的提取
- 确认是否具有某种结构
- …
- 模式集合
用给定的模式 P,在目标字符串 T 中搜索与模式 P 全 同的一个子串,并求出 T 中第一个和 P 全同匹配的子 串(简称为”配串”),返回其首字符位置

为使模式 P 与目标 T 匹配,必须满足
p0 p1 p2 ...pm-1 = ti ti+1 ti+2 ... ti+m-1
模式匹配的目标和算法:
- 目标:在大文本(诸如,句子、段落,或书本)中 定位(查找)特定的模式
- 解决模式匹配问题的算法
- 朴素(称为“Brute Force”,也称 “Naive” )
- Knuth-Morrit-Pratt ( KMP) 算法 )
- ……
一、朴素算法(穷举法)
设 T = t0t1, t2, …,tn-1,P = p0, p1, …, pm-1
- i 为 T 中字符的下标,j 为 P 中字符的下标
- 匹配成功 (p0 = ti , p1 = ti+1 , …, pm-1 = ti+m-1 ) ,即,T.substr(i, m) == P.substr(0, m)
- 匹配失败 (pj≠ti ) 时, •将 P 右移再行比较
- 尝试所有的可能情况



朴素模式匹配算法:其一

朴素模式匹配算法:其二

朴素模式匹配代码(简洁)

模式匹配原始算法:效率分析
假定目标 T 的长度为 n,模式 P 长度为 m,m≤n
- 在最坏的情况下,每一次循环都不成功,则一共要进行比较(n-m+1)次
- 每一次“相同匹配”比较所耗费的时间,是 P 和 T 逐个字符比较的时间,最坏情况下,共 m 次
- 因此,整个算法的最坏时间开销估计为O( m * n )
朴素模式匹配算法:最差情况
模式与目标的每一个长度为 m 的子串进行比较
- 目标形如 an-1 X
- 模式形如 am-1b
总比较次数: m(n – m + 1)
时间复杂度: O(mn)
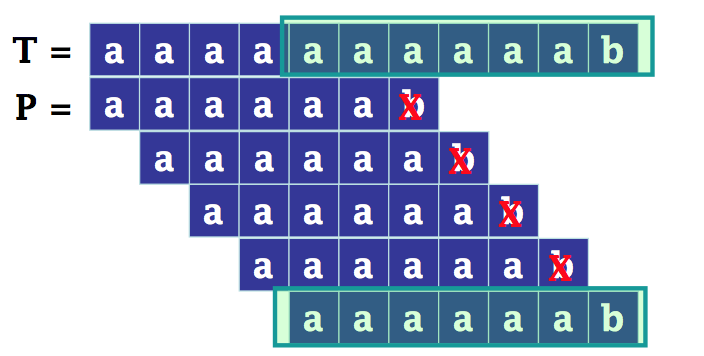
最佳情况-找到模式
在目标的前 m 个位置上找到模式,设 m = 5

总比较次数:m
时间复杂度:O(m)
最佳情况-没找到模式
- 总是在第一个字符上不匹配
- 总比较次数: n–m+1
- 时间复杂度: O(n)
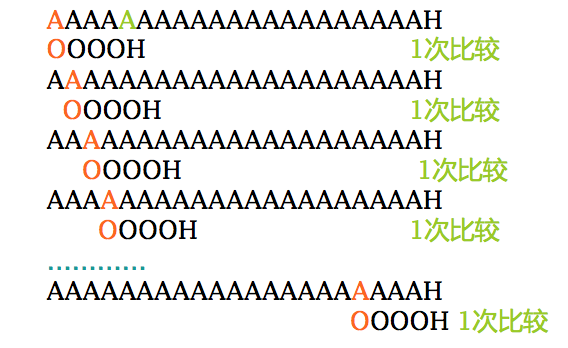
朴素算法的冗余运算
朴素算法之所以较慢的原因是有冗余运算
e.g.
- 由1)可知: p5 ≠ t5, p0 ≠t0, p1 = t1,同时由 p0 ≠ p1可得知p0 ≠t2 故将 P 右移一位后第2) 趟比较一定不等; 比较冗余
- 那么把 P 右移几位可以消除冗余的比较而不丢 失配串呢?

二、KMP算法
无回溯匹配
匹配过程中,一旦 pj 和 ti 比较不等时,即
P.substr(1,j-1) == T.substr(i-j+1,j-1)
但 pj ≠ ti
- 该用 P 中的哪个字符 pk 和 ti 进行比较?
- 确定右移的位数
- 显然有k<j,且不同的j,其k值不同
Knuth-Morrit-Pratt (KMP)算法 : k 值仅仅依赖于模式 P 本身,而与目标对象T无关
KMP算法思想

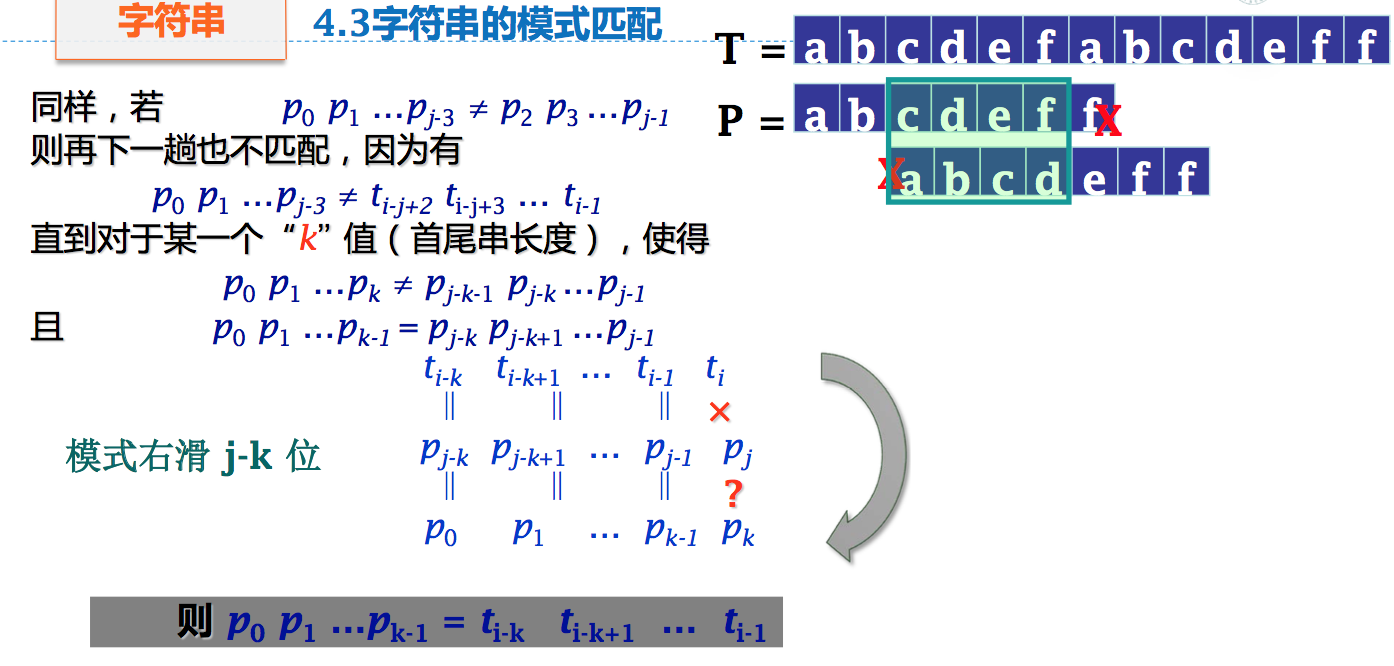
字符串的特征向量N
设模式 P 由 m 个字符组成,记为 P = p0 p1p2p3……pm-1
令 特征向量 N 用来表示模式 P 的字符分布特征,简称 N 向量由m个特征数 n0 …nm-1 整数组成,记为 N = n0n1n2n3……nm-1
N 在很多文献中也称为 next 数组,每个 nj 对应 next 数组中的元素 next[j]
字符串的特征向量N:构造方法:
P 第 j 个位置的特征数 nj,首尾串最长的 k
- 首串: p0 p1 … pk-2 pk-1
- 尾串: pj-k pj-k+1 … pj-2 pj-1
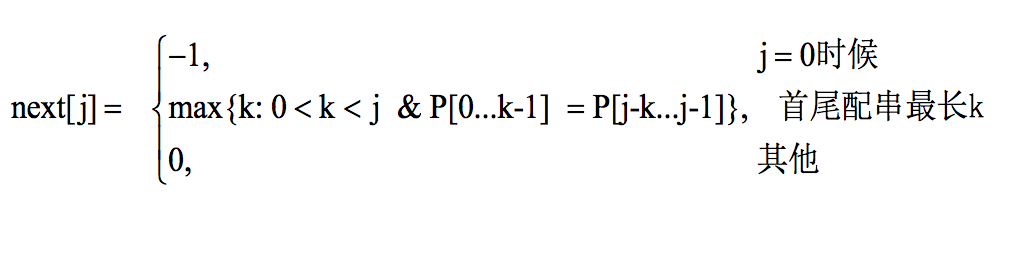

KMP模式匹配示例
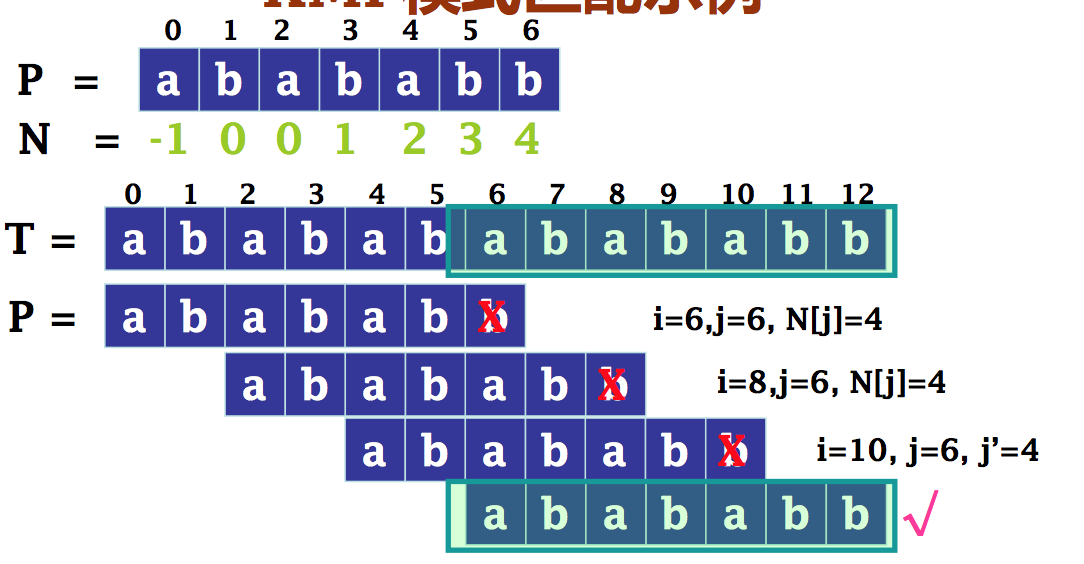
KMP模式匹配算法

对应的求特征向量算法框架:
特征数 nj ( j>0, 0≤ nj+1≤ j )是递归定义的, 定义如下:
- n0 = -1,对于j > 0的 nj+1 ,假定已知前一位置的 特征数nj,令k=nj ;
- 当k≥0且pj≠pk 时,则令k=nk;让步骤2循 环直到条件不满足
- nj+1 =k+1;//此时,k==-1或pj ==pk
字符串的特征向量N ——非优化版:

求特征向量N



字符串的特征向量N ——优化版

next数组对比
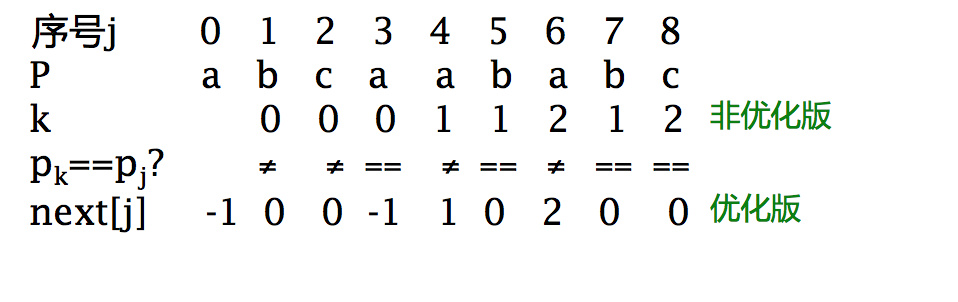
KMP算法的效率分析
循环体中”j = N[j];” 语句的执行次数不能超过 n 次。否则,
- 由于“j = N[]; ”每执行一次必然使得j减少(至少减1)
- 而使得 j 增加的操作只有“j++ ”
- 那么,如果“j = N[j]; ”的执行次数超过n次,最终的结果必然 使得 j 为比-1小很多的负数。这是不可能的(j有时为-1,但是 很快+1回到0)。
- 同理可以分析出求N数组的时间为O(m) 故,KMP算法的时间为O(n+m)
总结:单模式的匹配算法:

思考:不同版本特征值定义

更多阅读
- Pattern Matching Pointer – http://www.cs.ucr.edu/~stelo/pattern.html
- EXACT STRING MATCHING ALGORITHMS – http://www-igm.univ-mlv.fr/~lecroq/string/ – 字符串匹配算法的描述、复杂度分析和C源代码
参考资料
北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾
