【11.6】索引--红黑树

BST的平衡问题：

• 理想状况:插入、删除、查找时间代价为O(logn )
• 输入9,4,2,6,7,15,12,21
• 输入2,4, 6,7, 9, 12,15, 21

一、红黑树定义:red-black tree, 简称RB-tree

红黑树:平衡的 扩充 二叉搜索树

• 颜色特征:结点是“红色” 或“黑色”;
• 根特征 :根结点永远是“黑色”的;
• 外部特征:扩充外部叶结点都是空的“黑色” 结点;
• 内部特征:“红色”结点的两个子结点都是 “黑色”的，丌允许两个连续的红色结点;
• 深度特征:任何结点到其子孙外部结点的每条 简单路径都包含相同数目的“黑色”结点

红黑树的阶

• 结点X的阶(rank，也称“黑色高度”)
• 从该结点到外部结点的黑色结点数量
• 不包括 X 结点本身，包括叶结点
• 外部结点的阶是零
• 根的阶称为该树的阶

二、 红黑树相关性质

1. 红黑树是满二叉树 ，空叶结点也看作结点
2. 阶为 k 的红黑树路径长度：最短是 k，最长是 2k。从根到叶的简单路径长度： 阶为 k 的红黑树树高最小是 k+1，最高是 2k+1
3. 阶为k的红黑树的内部结点 最少是一棵完全满二叉树，内部结点数最少是 2^k-1
4. n 个内部结点的红黑树树高 最大是 $ 2 log_{2} (n+1)+1 $

证明:

• 设红黑树的阶为 k，设红黑树的树高是 h。
• 由性质(2) 得 h <= 2k+1，则 k >= (h-1) / 2
• 由性质(3)得 n>=2^k–1,即n>=2^(h-1)/2 –1
• 可得出 h <= $ 2 log_{2} (n+1)+1 $

三、结点插入算法

• 先调用 BST 的插入算法
• 把新记录着色为红色
• 若父结点是黑色，则算法结束
• 否则，双红调整

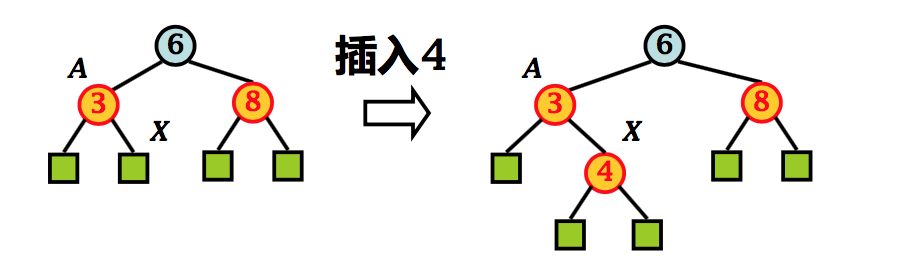
3.1 插入算法调整 1:重构

情况1:新增结点 X 的叔父结点是黑色

每个结点的阶都保持原值，调整完成

4 种形式的结构调整

原则:保持 BST 的中序性质

3.2 插入算法调整 2:换色

情况 2:新增结点 X 的叔父结点也是红色

需要继续检查平衡

插入 4

• 情况 2 红红冲突 。 父和叔父也是红
• 父祖换色

情况 1 红红冲突。 叔父是黑 。 重构

四、结点删除算法

• 先调用 BST 的删除算法

• 待删除的结点有一个以上的外部空指针，则直接删除

• 否则在右子树中找到其后继结点进行值交换(着色不变)删除

• v 是被删除的内结点, w 是被删外结点, X 是 w 的兄弟

• 如果v或者 X 是红色, 则把X标记为黑色即可 *否则, X 需要标记为双黑, 根据其兄弟结点 C 进行重构调整

4.1 根据双黑 X 的兄弟 C 进行调整

假设X是左子结点(若X为右孩子，则对称)

• 情况 1: C 是黑色，且子结点有红色

• 重构，完成操作

• 情况 2: C 是黑色, 且有两个黑子结点

• 换色

• 父结点 B 原为黑色，可能需要从 B 继续向上调整

• 情况3: C是红色

• 转换状态

• C 转为父结点，调整为情况 1 或 2 继续处理

4.1.1 情况 1(a) 重构:侄子红结点八字

• 将兄弟结点 C 提上去
• C 继承原父结点的颜色
• 然后把B着为黑色，D 着为黑色，其他颜色不变即可

4.1.2 情况 1(b) 重构:侄子红结点同边顺

• 将 D 结点旋转为 C 结点的父结点，D 继承原 子根 B 的颜色，B 着为黑色

4.1.3 情况 2:兄弟是黑色, 且有两个黑子结点

• 把 C 着红色， B 着黑色
• 如果 B 原为红色，则算法结束
• 否则，对 B 继续作“双黑”调整

4.1.4 情况 3: 兄弟 C 是红色

• 旋转
• X 结点仍是“双黑”结点，转化为前面2种情况

4.1.5 例子

删除 90

• 当前结点变为 80 的右黑叶结点
• C 是黑色, 且有两个黑色子结点:情况 2

情况 2 换色

删除 70

红结点，不要调整

删除 80

• 当前结点 X 变为 65 的右黑叶结点 * C 是红色:情况 3 状态转换

删除 80(调整)

• C 是黑色，且左黑、右红:情况 1(b) 重构

完成调整

4.2 删除操作时间代价

• 其平均和最差检索 O(log2 n)
• 自底向根的方向调整
• 红黑树构造
• (数据，左指针，右指针，颜色，父指针)
• 自顶向下的递归插入/删除调整方
• (数据，左指针，右指针，颜色)
• 若非递归，则记录回溯路径

4.3 从 Red-Black-Tree 到 2-3-4 树

• 假设将一棵红黑树的每个红结点“吸收”到他的黑色父 结点中，来让红结点的子女变为黑色父结点的子女(忽 略关键字的变化)

• 当一个黑结点的所有红色子女都被吸收后， 其可能的度是多少?

• 2、3、4 即成为一棵 2-3-4 树(阶为 4 的 B 树)

• 此结果树的叶子深度怎样? 叶结点等高

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾