【12.5.2】高级数据结构--改进的二叉搜索树(伸展树)

• 一种自组织数据结构
• 数据随检索而调整位置
• 汉字输入法的词表
• 伸展树不是一个新数据结构，而只是改进 BST 性能的一组规则
• 保证访问的总代价不高，达到最令人满意的性能
• 不能保证最终树高平衡

一、展开 (splaying)

• 访问一次结点 (例如结点 x) ，完成一次称为展开的过 程
• x 被插入、检索时，把结点 x 移到 BST 的根结点
• 删除结点 x 时，把结点 x 的父结点移到根结点
• 像在 AVL 树中一样，结点x的一次展开包括一组旋转 (rotation)
• 调整结点 x、父结点、祖父结点的位置
• 把 x 移到树结构中的更高层

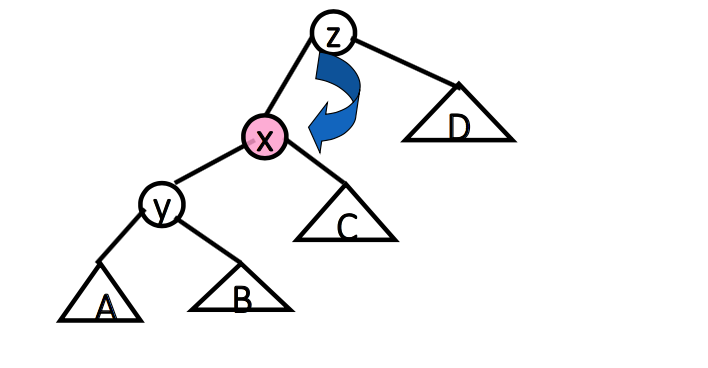
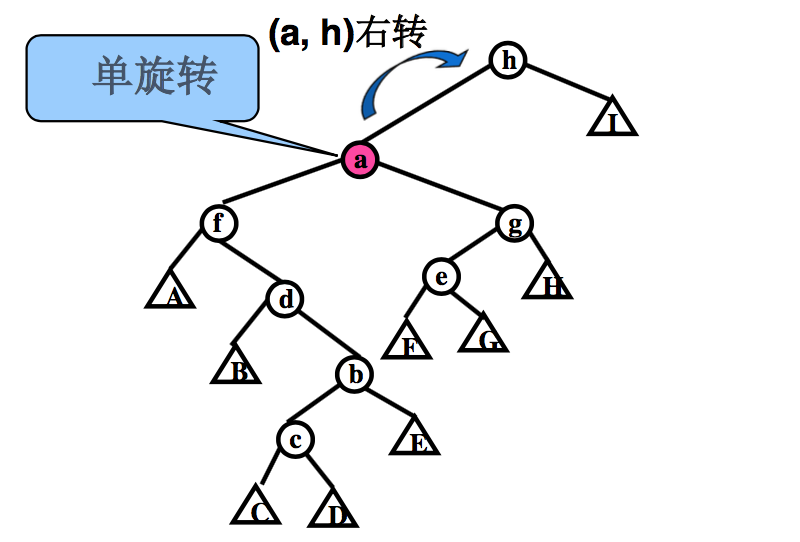
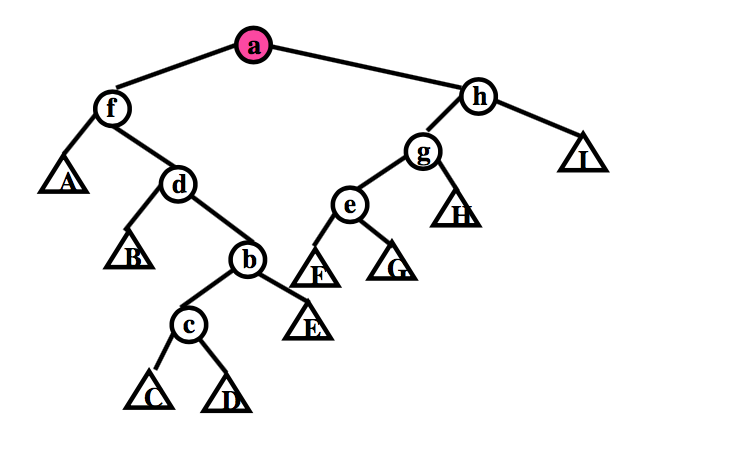
二、单旋转 (single rotation)

• x 是根结点的直接子结点时
• 把结点 x 与它的父结点交换位置
• 保持 BST 特性

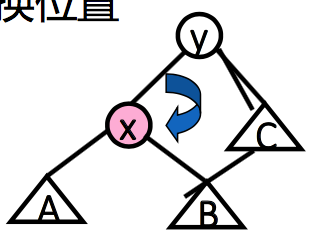
x、y 为内部结点编号，不是值大小

A、B、C 代表子树，有大小顺序

三、双旋转 (double rotation)

• 双旋转涉及到
• 结点 x
• 结点x的父结点(称为y)
• 结点 x 的祖父结点 (称为 z)
• 把结点 x 在树结构中向上移两层
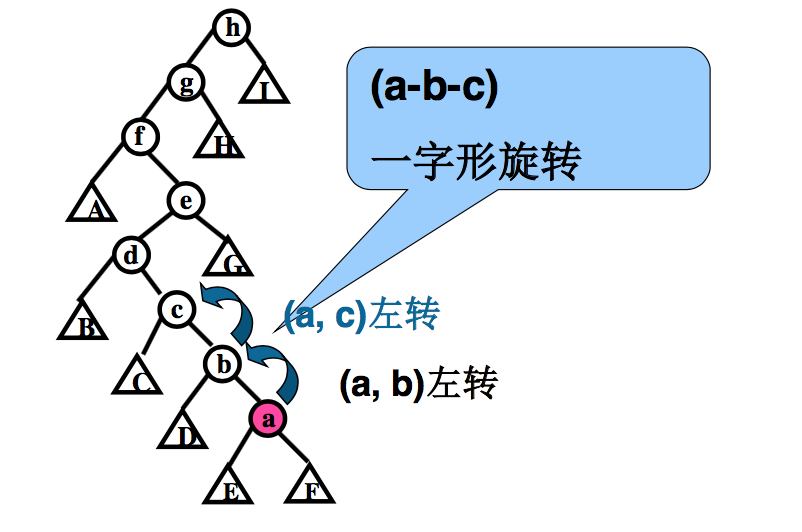
• 一字形旋转 (zigzig rotation)
• 也称为同构调整 (homogeneous configuration)
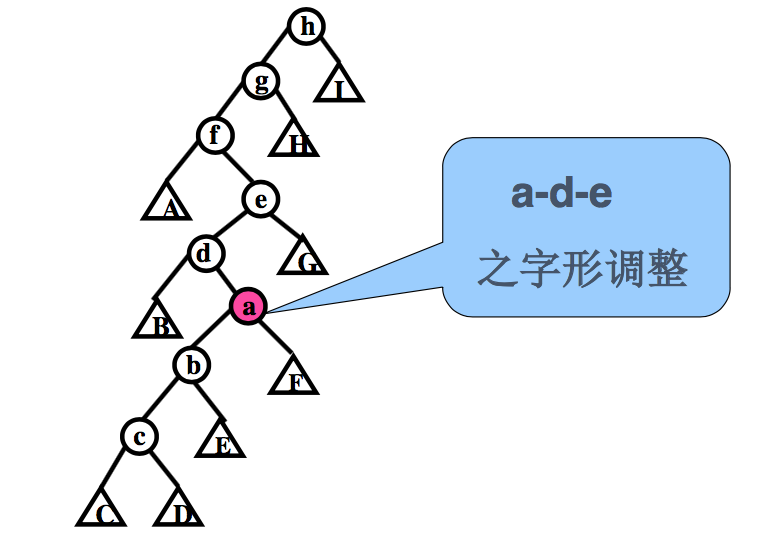
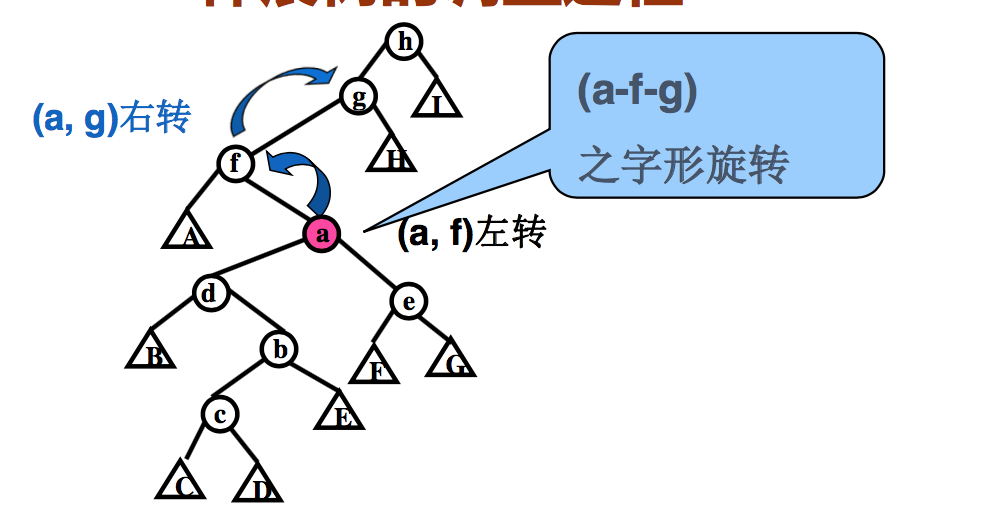
• 之字形旋转 (zigzag rotation)
• 也称为异构调整 (heterogeneous configuration)

3.1 一字形旋转图示

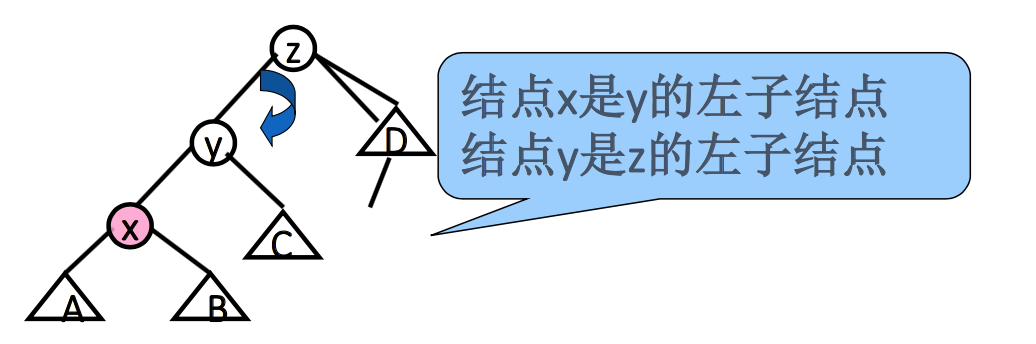
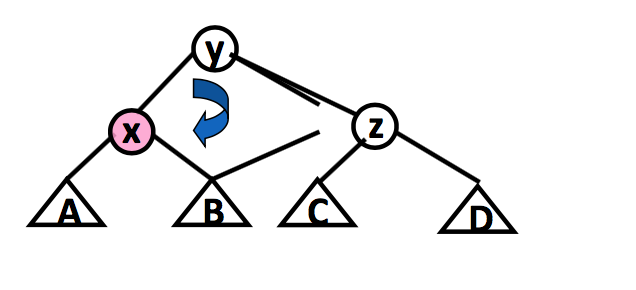
3.2 之字形旋转图示

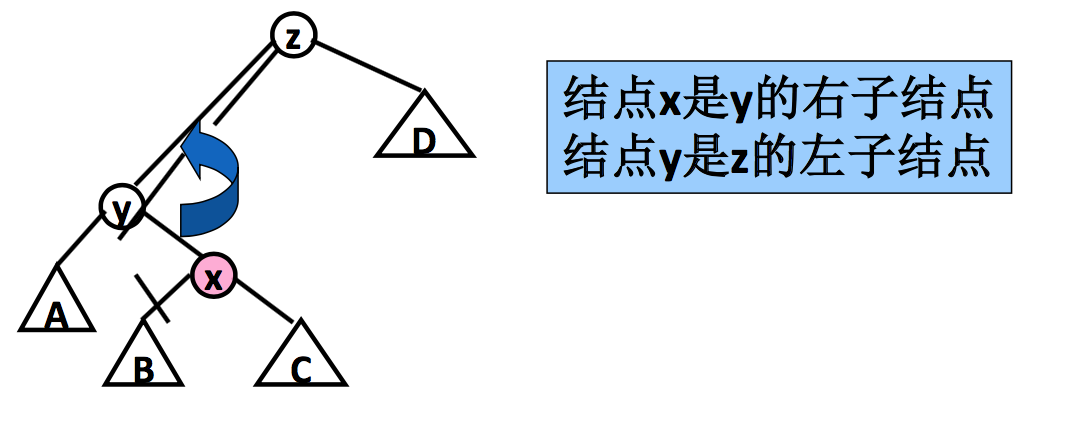
3.3 两种旋转的不同作用

• 之字形旋转
• 把新访问的记录向根结点移动
• 使子树结构的高度减1
• 趋向于使树结构更加平衡
• 一字形提升
• 一般不会降低树结构的高度
• 只是把新访问的记录向根结点移动

四、伸展树的调整过程

• 一系列双旋转
• 直到结点 x 到达根结点或者根结点的子结点
• 如果结点x到达根结点的子结点
• 进行一次单旋转使结点 x 成为根结点
• 这个过程趋向于使树结构重新平衡
• 使访问最频繁的结点靠近树结构的根层
• 从而减少访问代价

五、伸展树与 AVL 树的差别

• 伸展树与结点被访问的频率相关
• 根据插入、删除、检索
• 动态地调整
• 而 AVL 树的结构与访问频率无关
• 只与插入、删除的顺序有关

六、伸展树的效率

• n 个结点的伸展树
• 进行一组m次操作 (插入、删除、查找操作) ，当 m≥n时，总代价是 O(m logn)
• 伸展树不能保证每一个单个操作是有效率的
• 即每次访问操作的平均代价为O(logn)
• 不要求掌握证明方法

七、思考

• 全伸展与半伸展树的特点及应用?
• 对比红黑树、AVL 树、Splay 树的平 衡策略，哪个更好?
• 最差情况下的树高
• 统计意义下的操作效率
• 代码的易写、易维护

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾