【2.6.1】向量相似性--余弦相似度(Cosine Similarity)
- 几何中,夹角余弦可用来衡量两个向量方向的差异
- 机器学习中,借用这一概念来衡量样本向量之间的差异。

二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
$$ cosθ = \frac{ x_{1}x_{2} + y_{1}y_{2} }{\sqrt{ x_{1}^{2} +y_{1}^{2} }\sqrt{ x_{2}^{2} +y_{2}^{2} }}$$
两个n维样本点a(x1,x2,…,xn)和b(y1,y2,…,yn)的夹角余弦为:
$$ cos(θ) = \frac{a*b}{|a||b|} = \frac{ \sum \limits_{i=1}^{n}(x_{i} * y_{i})}{ \sqrt{ \sum \limits_{i=1}^{n}(x_{i})^{2}} \sqrt{ \sum \limits_{i=1}^{n}(y_{i})^{2} } }$$
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小,余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1。
二、案例
2.1 余弦计算文本相似度
- 句子A:这只皮靴号码大了。那只号码合适
- 句子B:这只皮靴号码不小,那只更合适
怎样计算上面两句话的相似程度?
基本思路是:如果这两句话的用词越相似,它们的内容就应该越相似。因此,可以从词频入手,计算它们的相似程度。
第一步,分词。
- 句子A:这只/皮靴/号码/大了。那只/号码/合适。
- 句子B:这只/皮靴/号码/不/小,那只/更/合适。
第二步,列出所有的词。
这只,皮靴,号码,大了。那只,合适,不,小,很
第三步,计算词频。
-
句子A:这只1,皮靴1,号码2,大了1。那只1,合适1,不0,小0,更0
-
句子B:这只1,皮靴1,号码1,大了0。那只1,合适1,不1,小1,更1
第四步,写出词频向量。
- 句子A:(1,1,2,1,1,1,0,0,0)
- 句子B:(1,1,1,0,1,1,1,1,1)
到这里,问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段,都是从原点([0, 0, …])出发,指向不同的方向。两条线段之间形成一个夹角,如果夹角为0度,意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等;如果夹角为90度,意味着形成直角,方向完全不相似;如果夹角为180度,意味着方向正好相反。因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
计算两个句子向量
- 句子A:(1,1,2,1,1,1,0,0,0)
- 和句子B:(1,1,1,0,1,1,1,1,1)
的向量余弦值来确定两个句子的相似度。
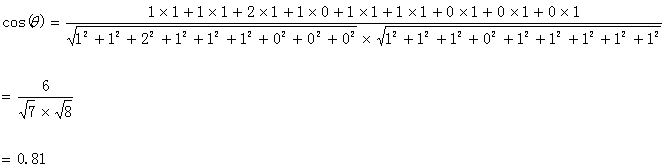
计算结果中夹角的余弦值为0.81非常接近于1,所以,上面的句子A和句子B是基本相似的
由此,我们就得到了文本相似度计算的处理流程是:
- 找出两篇文章的关键词;
- 每篇文章各取出若干个关键词,合并成一个集合,计算每篇文章对于这个集合中的词的词频
- 生成两篇文章各自的词频向量;
- 计算两个向量的余弦相似度,值越大就表示越相似。
三、讨论
欧氏距离和余弦相似度的区别
从上图可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
吴军. 数学之美 系列 12 -余弦定理和新闻的分类.(一个比较好的栗子)
http://www.google.com.hk/ggblog/googlechinablog/2006/07/12_4010.html
参考资料
