【2.4.2】编辑理论--汉明距离(hamming-distance)
汉明距离是使用在数据传输差错控制编码里面的,汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,我们以d ( x , y ) 表示两个字x , y 之间的汉明距离。对两个字符串进行异或运算,并统计结果为1 的个数,那么这个数就是汉明距离。

一、 汉明距离的定义
在信息理论中,Hamming Distance 表示两个等长字符串在对应位置上不同字符的数目,我们以d(x, y)表示字符串x和y之间的汉明距离。从另外一个方面看,汉明距离度量了通过替换字符的方式将字符串x变成y所需要的最小的替换次数。
# 举例说明以下字符串间的汉明距离为:
"karolin" and "kathrin" is 3.
"karolin" and "kerstin" is 3.
1011101 and 1001001 is 2.
2173896 and 2233796 is 3.
二、 汉明距离的意义
对于二进制串a和b来说,汉明距离等于aXORb中1的数目,我们又称其为汉明权重,也叫做population count或popcount。长度为n的二进制字符串通过汉明距离构成了一个度量空间(metric space),我们称其为汉明立方(Hamming Cube)。
下图表示在hypercube中 0100→1001 (红色)的汉明距离是 3; 0110→1110 (蓝色)的汉明距离是 1
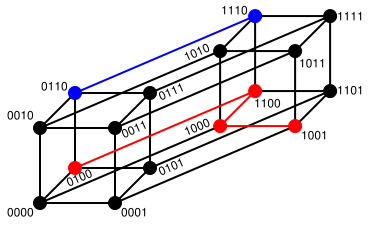
汉明权重:是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是 1 的个数,所以 11101 的汉明重量是 4。因此,如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
三、 汉明距离的计算
python3 简单计算汉明距离的代码如下:
def hammingDistance(s1, s2):
"""Return the Hamming distance between equal-length sequences"""
if len(s1) != len(s2):
raise ValueError("Undefined for sequences of unequal length")
return sum(el1 != el2 for el1, el2 in zip(s1, s2))
Wegner (1960) 提出了一种计算汉明权重(即计算给定整数的二进制表示中1的个数)的算法,通过反复查找并消除最低的非零bit位来实现
汉明距离多用于编码等信息论方面的计算,可视化的煮个栗子
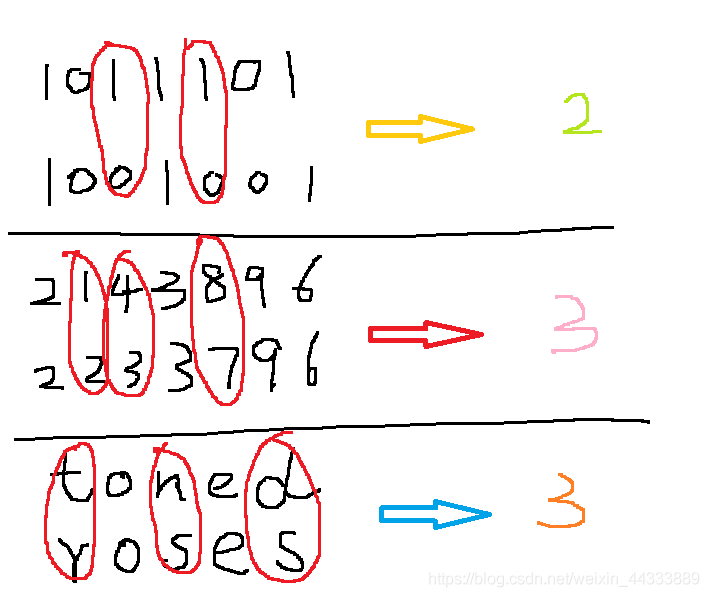
四、应用
汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中,为了增强容错性,应使得编码间的最小汉明距离尽可能大。但是,如果要比较两个不同长度的字符串,不仅要进行替换,而且要进行插入与删除的运算,在这种场合下,通常使用更加复杂的编辑距离等算法。
最小汉明距离:例如:(00)与(01)的距离是1,(110)和(101)的距离是2。在一个码组集合中,任意两个编码之间汉明距离的最小值称为这个码组的最小汉明距离。最小汉明距离越大,码组越具有抗干扰能力。
参考资料
