点对互信息(PMI,Pointwise Mutual Information)
一、PMI(Pointwise Mutual Information)
机器学习相关文献中,可以看到使用PMI衡量两个变量之间的相关性,比如两个词,两个句子。原理公式为:
$$ PMI(x;y) = log\frac{p(x,y)}{p(x)p(y)} = log\frac{p(x|y)}{p(x)} = log\frac{p(y|x)}{p(y)} $$
在概率论中,如果x和y无关,p(x,y)=p(x)p(y);如果x和y越相关,p(x,y)和p(x)p(y)的比就越大。从后两个条件概率可能更好解释,在y出现的条件下x出现的概率除以单看x出现的概率,这个值越大表示x和y越相关。
log取自信息论中对概率的量化转换(对数结果为负,一般要再乘以-1,当然取绝对值也是一样的)
二、自然语言处理中使用PMI的例子
比如,要衡量like这个词的极性(正向情感or负向情感)。先选一些正向情感词如good,计算like跟good的PMI,
$$ PMI(like;good) = log\frac{p(like,good)}{p(like)p(good)} $$
其中p(like,good)表示like跟good在同一句话出现的概率(like跟good同时出现次数/总词数^2),p(like)表示like出现概率,p(good)表示good出现概率(good出现次数/总词数)。
p(like,good)表示like跟good在一句话中同时出现的概率(like跟good同时出现的次数除以N2)
PMI(like,good)越大表示like的正向情感倾向就越明显。
三、利用PMI预测对话的回复语句关键词
先在比较大的训练预料中计算query每个词(wq)和reply每个词(wr)的PMI
$$ PMI(w_{q};w_{r}) = log\frac{ p(w_{q},w_{r}) }{ p(w_{q})p(w_{r}) } = log\frac{p(w_{q}|w_{r})}{p(w_{q}))} $$
这里概率p(wq,wr)为wq和wr分别在一个对话pair的上下句同时出现的概率(wq和wr同时出现的对话pair数/训练语料q部分每个词和r部分每个词组成pair的总数),p(wq)是wq在q语句中出现的概率(wq在q语料中出现的语句数/q语料总数)。
计算出一个PMI矩阵,两个维度分别是query词表和reply词表,
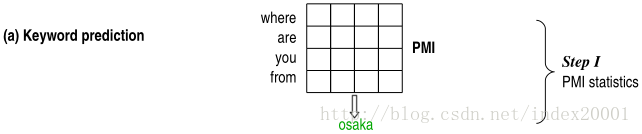
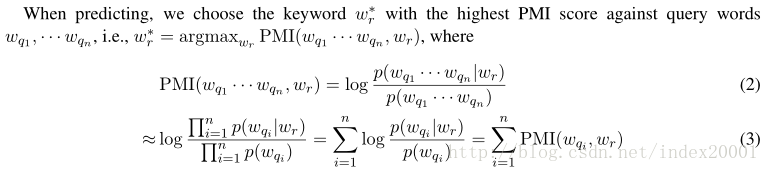
预测回复关键词时,计算候选词表中某个词和给定的query的n个词(wq1,…wqn)的PMI,对n求和,候选词表每个词都这样求个PMI和,选出最大的那个对应的候选词就是predict word。
文章中还对 keyword candidates作了限制,规定它的范围是名词。
举个栗子
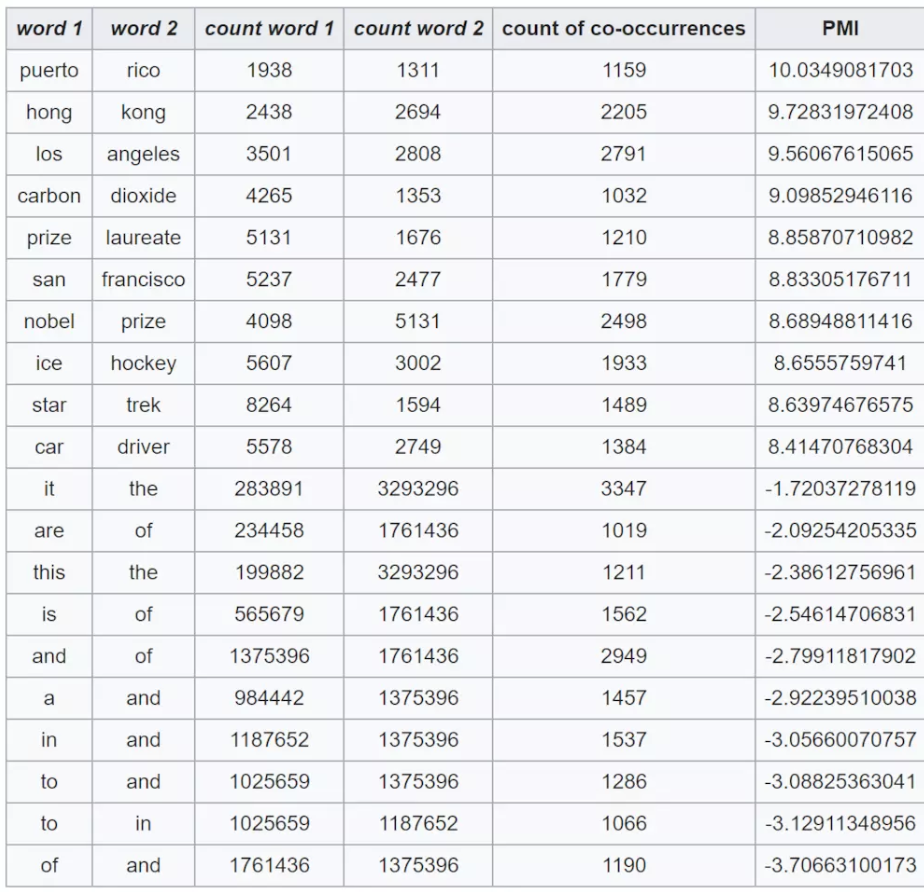
The following table shows counts of pairs of words getting the most and the least PMI scores in the first 50 millions of words in Wikipedia (dump of October 2015) filtering by 1,000 or more co-occurrences. The frequency of each count can be obtained by dividing its value by 50,000,952. (Note: natural log is used to calculate the PMI values in this example, instead of log base 2)
参考资料
