排序【3】--CA对应分析
一、背景
因子分析方法分为R型因子分析和Q型因子分析。R型因 子分析研究变量(指标)之间的相关关系,Q型因子分析研究 样本之间的相关关系。
有时不仅关心变量之间或样本之间的相关关系,还关心变 量和样本之间的对应关系,这是因子分析方法所不能解释的。

对应分析(Correspondence analysis)也称关联分析、R-Q型因子分析,也叫做相互平均法(Reciprocal averaging, RA),是近年新发展起来的一种多元相依变量统计分析技术,通过分析由定性变量构成的交互汇总表来揭示变量间的联系。CA/RA的模型为单峰模型。因此,它们的分析结果一般优于PCA,在样地数据参数较大的情况下尤为如此.
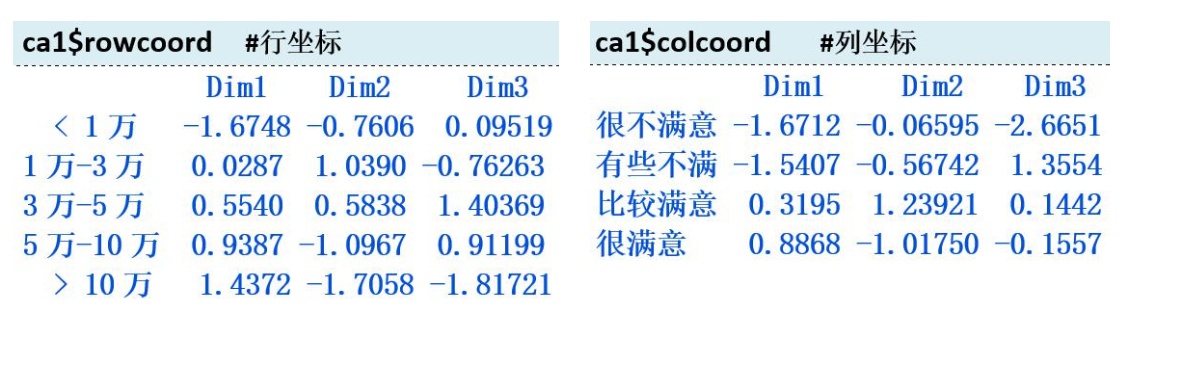
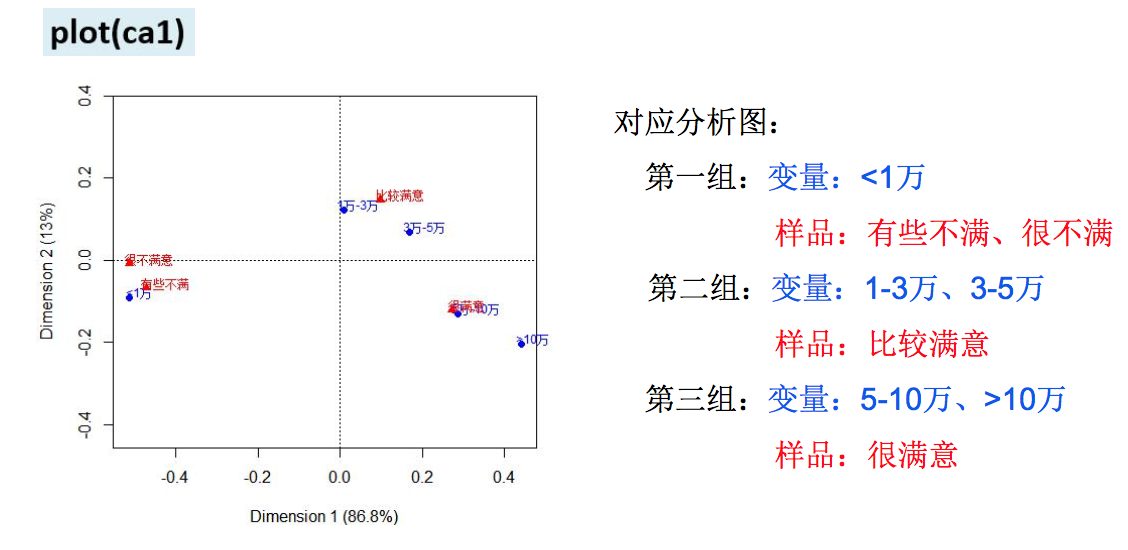
通俗点说,就是将行的编号以及列的编号在一个二维坐标轴中做出相应的点,可以看到行编号以及列编号对应的距离关系来看行之间,列之间,行与列之间的关系,距离越近,关系越密切,同时根据特征值,来判断某个点对整个数据的贡献情况。
二、对应分析的基本原理
对应分析的作用:
对应分析是分析两组或多组因素之间关系的有效方法, 在离散情况下,建立因素间的列联表来对数据进行分析
什么情况下进行对应分析;
对数据作对应分析之前,需要先了解因素间是否独立, 如果因素之间相互独立,则没有必要进行对应分析
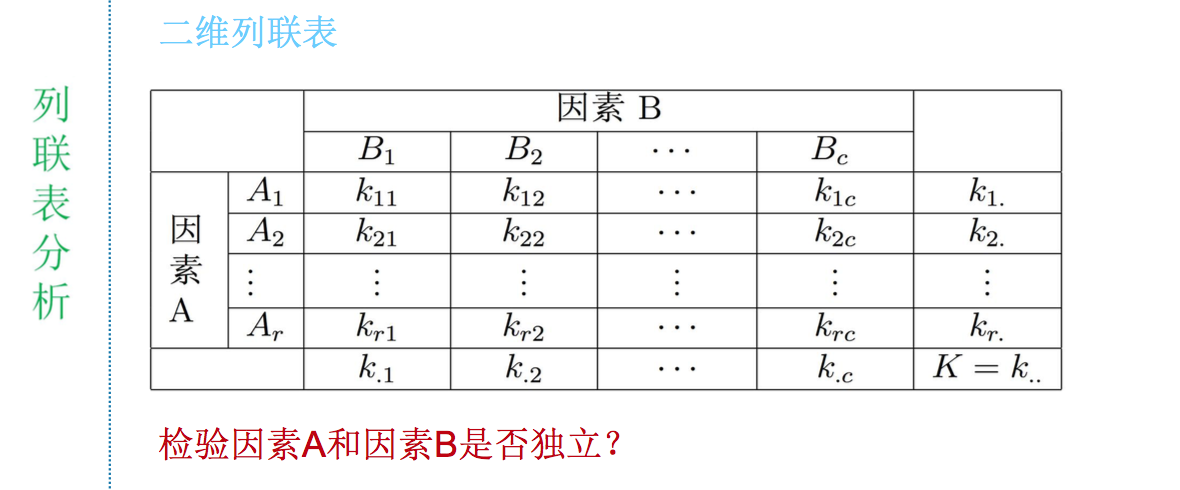

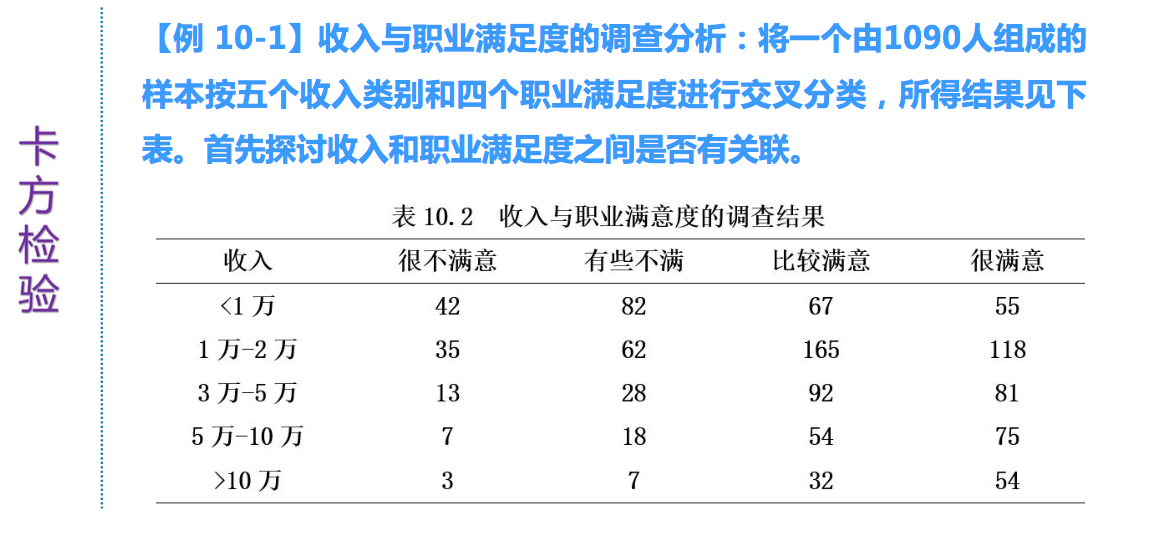



三、对应分析的计算步骤
3.1 具体算法
Inertia-惯量, 为每一维到其重心的加权距离的平方。它度量行列关系的强度。 Singular Value-奇异值(是惯量的平方根),反映了是行与列各水平在二维图中分量的相关程度,是对行与列进行因子分析产生的新的综合变量的典型相关系数。 Chi Square-就是关于列联表行列独立性c2检验的c2统计量的值,和前面表中的相同。其后面的Sig为在行列独立的零假设下的p-值,注释表明自由度为(4-1)×(3-1)=6,Sig.值很小说明列联表的行与列之间有较强的相关性。 Proportion of Inertia-惯量比例,是各维度(公因子)分别解释总惯量的比例及累计百分比,类似于因子分析中公因子解释能力的说明。
同样我们用虚拟例子来说明计算过程。假定我们调查得到5个样方4个种的数据矩阵:
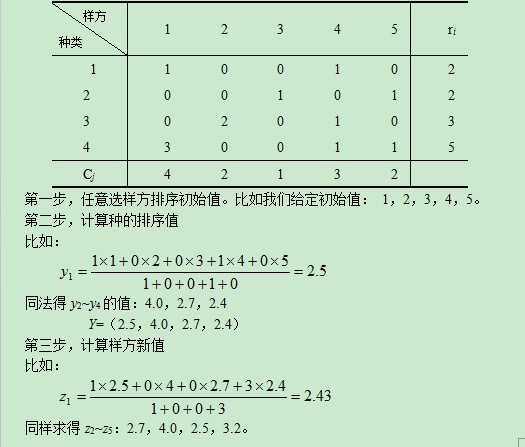

然后,同第一轴一样进行标准化,重复迭代过程。因为这一组初始值选的比较佳,只进行三次就可以得到稳定的结果。 样方在第二轴上的排序值为: -1.073,1.393,1.751,-0.262,0.348,(λ=0.598)。 种类在第二轴上的排序值为: -0.647,1.045,0.836,0.632。

CA/RA的模型是非线性的,排序明显优于PCA,这一点在研究中得到了广泛的证实。因此,使用较为普遍。但它有一个重大缺点,就是CA/RA的第二排序轴在许多情况下是第一轴的二次变形,即所谓的“弓形效应”(Arch effect)或者“马蹄形效应”(horse—shoe effect)。如图9. 16所示, 18个样方在第二轴上的坐标与第一轴的坐标是二次曲线关系,这是由于正交化的必然结果(Gauch 1982)。弓形效应也可以从图9.14中明显的看出来。弓形效应对排序的精度有所影响(Hill和Gauch 1980;Gauch 1982;Greig—Smith 1983)。
3.2 算法及R的使用
Q型与R型因子分析分别反映了数据的不同方面,他们之间必然有 内在的联系,对应分析通过巧妙的数学转换,将Q型和R型因子分析 有机地结合起来。


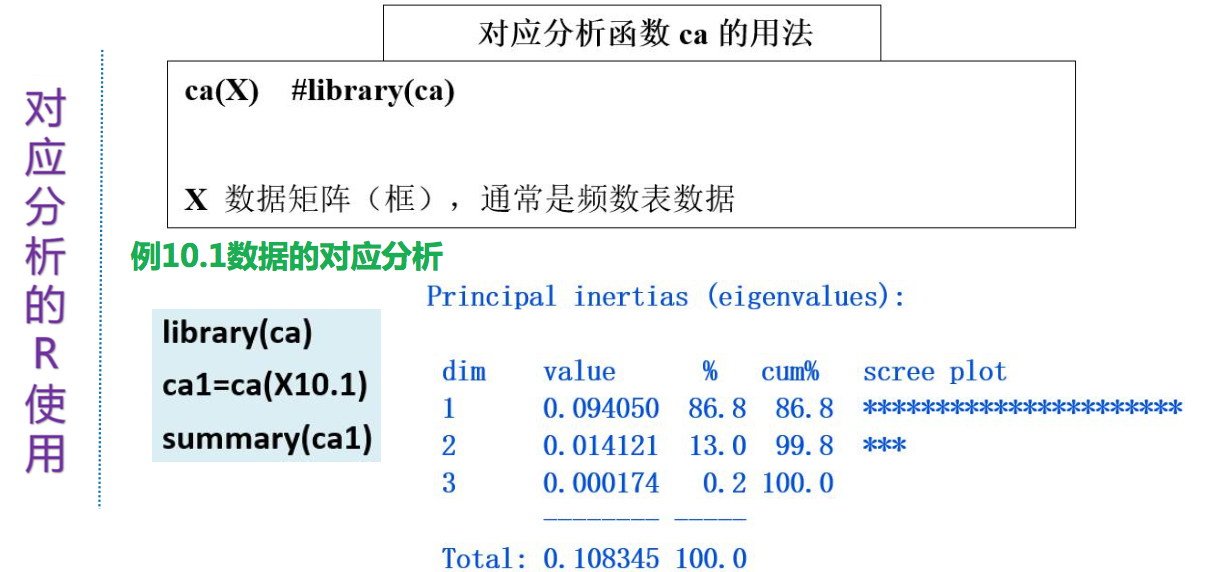


四、注意的问题
- 不能用于相关关系的假设检验
- 维度由变量所含的最小类别决定
- 对极端值敏感性研究
- 研究对象要有可比性
- 变量的类别应涵盖所有情况
- 不同标准化分析的结果不同
参考资料:
- http://pan.baidu.com/s/1jGJtCzW
- http://pan.baidu.com/s/1ntJTzNb
- http://pan.baidu.com/s/1kTupcsJ
- 暨南大学 王斌会老师 《多元统计分析及R语言建模》课件
