【2.1】成分分析
很好的资料
一、Introduction to Compositional Analysis(成分分析导论)
1.1 什么是成分数据?
根据韦伯斯特第二版新大学词典,作文是“将部分或元素组合在一起形成一个整体的行为”,或者是“这些部分组合或相关的方式:构成”。成分数据定量地描述了整体的各个部分,并且只提供了它们的组成部分之间的相关信息。因此,成分数据以整体或部分总量的比例或分数存在,只传达相对信息,并且具有以下特性:
- 组成元素是非负的
- 并且总和是统一的。
从实践的角度来看,如果研究人员真的只对相对频率感兴趣,而不是对数据的绝对量感兴趣,那么这些数据就是成分数据。因此,成分数据经常出现在不同的科学领域:基因组学、种群遗传学、人口学、生态学、生物学、化学、地质学、岩石学、沉积学、地球化学、行星学、心理学、市场营销学、调查分析、经济学、概率和统计学。
1.2 Aitchison Simplex
从数学上讲,如果一个数据包含D个和为1的多个非负数部分或任何常数和约束。它可以正式地表述为:
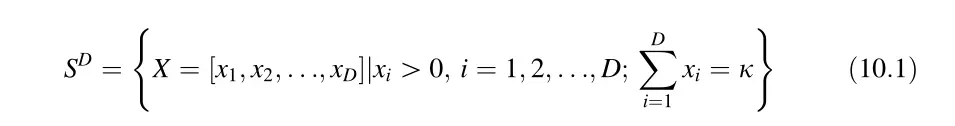
该公式指出,成分数据可以用具有正分量的常数和实向量来表示。这将成分数据的样本空间定义为一个超平面,称为单纯形。请注意,k是任意的。根据测量单位或重新缩放的不同,频繁值为1 (per unit, proportions), 100 (percent, %), 10^6(ppm, parts permillion), and 10^9(ppb, parts per billion)。
1.3 关于标准统计方法的问题
标准的数据分析技术,如相关分析,依赖于真实空间中Euclidean几何的假设。将它们应用于成分数据可能会产生误导结果,因为成分数据表示样本空间单纯形的特殊属性。在第3章“成分数据的统计分析”回顾和讨论了成分数据分析中的一些具有挑战性的问题。我们在这里总结了要点,并给出了进一步的解释。首先,有一个虚假的相关性,这导致很难以任何有意义的方式解释比例之间的相关性,主要是因为不相关的比例不一定是独立的。早在1897年,pearson首先观察到变量比率之间的“伪相关”问题。即,虽然统计上独立的变量X、Y和Z不相关,但它们的比率X/Z和Y/Z必须是相关的,因为它们的公约数。例如,在微生物组研究中,相对丰富的数据可以使统计上独立的分量似乎是相关的。因此,相对丰度的关联被认为是错误的,而相对丰度的相关分析完全不能告诉我们任何事情。其次,在成分数据分析中出现了高维的困难,这导致了多变量变异性模式的图形扭曲。当分析局限于选择几个子成分而不是作为整体的成分时,它就会投射出部分分析,从而失去多变量变异性模式的图景。由于单位和约束将组成矢量限制在一个单纯形中,因此发生了图形失真:在熟悉的空间(如R2)中看到的图形模式不能保证是相同的。第三,常和问题(也称为负偏差问题)使得用通常的方法解释相关性和协方差变得困难。传统的方法是通过乘积矩协方差来表示D部分合成向量的组成之间的相互依赖关系。然而,协方差结构是不可解释的。这些困难有多种表现形式:否定偏向困难、次成分困难、基础困难和零关联困难。受单位和或常和约束的约束,(原始)协方差矩阵的每行中必须至少有一个负元素。换句话说,它的条目中至少有D个必须是负数。例如,在每个样本中,如果生态系统中某一种分类群的数量增加,则其他一种或多种分类群的数量必须减少。因此,在协方差或相关矩阵的非负确定性的约束下,相关的值不在通常的区间内(−1,1)。这就是所谓的负偏向难度。类似地,单位和约束排除了子合成的原始协方差矩阵与完整合成的原始协方差矩阵之间的关系。此外,当我们从全组成转移到它的子组成时,原始相关性可能会发生很大的变化,并且当我们形成子组成时,方差可能会显示出不同的和不相关的排序。艾奇森称这为副作曲难度。当我们从基向量构造合成时,构造向量元素之间的相关性与它们的基向量不同,这导致很难将合成的原始协方差矩阵与其基的协方差矩阵联系起来:基难度。此外,由于负偏差,很难使用零值来表示随机变量的无相关性或独立性。实际上,碱基的不相关成分会产生零相关性,但不一定是零。这里的零相关概念类似于皮尔逊的伪相关。这是零关联难度。因此,成分约束因其对数据的协方差和相关结构的影响而臭名昭著。最后,利用单纯形样本空间中的参数分布对成分数据进行建模比较困难(参数建模困难)。回归多变量分析依赖于多元正态分布的假设,是在真实样本空间中进行的。与非负限制相比,单位和限制对组成成分的自由施加了更基本的限制。由于从整体或受非负约束和单位和约束对部件进行分析,由于值的范围有界,部件不能呈正态分布。因此,多元正态分布及其变换后的多元对数正态分布参数类不是分析成分数据的合适统计工具。在标准析因实验设计以及相关的方差分析和线性模型中,因素的独立性使我们能够检验它们对反应或特定交互作用项的加性效应。然而,在单纯形空间中,由于单位和的限制,因子(合成的D部分)不是独立的,实际上它们是混合物。如果我们改变一个组件,我们必须改变至少一个其他组件,并且不是线性的(特别是在边界)。因此,很难就混合物对响应的影响的性质提出有意义的假设。艾奇森称这是混合变种的困难。Aitchison给出的Dirichlet分布的主要性质是:Dirichlet组合的相关结构是完全负的,这使得分析某些Dirichlet组合的相关肯定为正的数据模式是不合适的。每一个Drichlet作品都有一个非常强的隐含独立性结构,不太可能用来描述即使是弱依赖形式的作品。因此,即使是Dirichlet类也完全不足以描述成分数据的可变性。总而言之,成分数据违反了所有标准统计检验的假设;即,部件之间的差异是线性的或相加的。它使大多数标准的统计方法和检验失效:(1)伪相关排除了相关分析;(2)图形失真使可视化工具(如散点图、QQ图等)失效。不可能;(3)成分的多变量正态性的缺乏排除了成分数据的多变量参数建模;以及(4)混合物的依赖性使得ANOVA和线性回归对于检验关于响应的假设没有意义。
1.4 成分数据的统计分析
基本原则:Aitchison提出了成分数据分析的三个基本原则,并建议我们在分析成分数据时应遵循这些原则。它们已数次重新配制根据微生物组分分析数据的新理论发展。这些原则都植根于成分数据的定义:只有成分的比率才能携带信息。
A 比例不变性:它指出,分析必须将具有比例正分量的向量视为代表相同的成分。换句话说,关于成分数据的统计推断不应该依赖于所使用的尺度。因此,单位向量和百分比向量传达的信息完全相同。我们应该从分析比例和百分比中得到完全相同的结果。例如,向量a=[11,2,5],b=[110,20,50]和c=[1100,200,500]由于其组成部分之间的相对重要性(比率)是相同的,所以它们的组成都是相同的.
B 亚成分连贯性:它指出,分析应仅依赖于关于该子集内的组件(或部件)的数据,而不应依赖于其他不涉及的组件(或部件);并且关于子组成(组件的特定子集)的统计推断应该是一致的,无论推断是基于子组成还是基于完整组成。
C 排列不变性:它指出,成分分析的结论不应取决于成分(部件)的顺序(顺序)。在成分分析中,来自不同组分顺序的信息不起作用。例如,我们选择哪个组件是“第一个”,哪个组件是“第二个”,以此类推,哪个是“最后”,这并不重要。
一族对数比变换(A Family of Log-Ratio Transformations):成分数据的主要问题是数据点不映射到Euclidean 空间,而是映射到Aitchison单纯形。问题是:如何分析成分数据?我们应该搬家,还是留在单纯的公寓里?因为标准的统计方法不能解决单纯形中的成分数据问题,所以成分数据分析的关键一步是提供一种在真实空间上进行一对一映射的方法。
A 对数和对数比转换(Log and Log-Ratio Transformations):在单纯形中解决成分数据问题的方法预计将通过几个步骤来完成:首先,使用对数比变换将成分转换到实空间,然后将标准统计方法应用于变换后的数据最后通过使用逆对数比变换返回到单纯形。成分数据的对数比变换被认为可以合法地恢复传统统计分析工具在相对丰度等情况下的大量使用。虽然使用对数比变换被认为是释放成分约束的关键方法,但要达到目前合适的版本需要很长时间。要消除成分数据中的非负约束,第一个也可能是最简单的方法是使用对数正态分布。一百多年来,从Galton-McAlister的介绍到Aitchison和Brown关于对数正态分布的教科书,对数变换技术随处可得。通过对数据进行对数变换,消除了非负约束,然后假设为正态分布。该方法类似于使用逻辑连接函数在广义线性模型框架下对二进制数据进行建模。然而,对数变换方法只解决了成分数据的非负约束,而没有解决单位和约束。直到20世纪80年代Aitchison提出了基于多种对数比变换的方法论,单位和约束问题才开始得到解决。艾奇逊在20世纪80年代意识到,构图只提供部件或部件的相对信息,而不是绝对值。因此,他使用成分比率来呈现关于作文的每一项陈述。因为在数学上对数比率比比率更容易处理,并且对数比率变换提供了到真实空间的一对一映射,所以它为研究人员开发基于各种对数比率变换的方法开辟了一条道路。对数比变换原理背后的算法是基于这样一个事实,即在成分向量和相关的对数比向量之间存在一一对应关系,因此关于成分的任何陈述都可以根据对数比进行改造,反之亦然。通过对数比变换,消除了约束样本空间(单纯形)的问题,并将数据投影到多变量实数空间。因此,开放所有可用的标准多变量技术。对数比转换方法被地质学、生态学和其他领域的统计学家和研究人员接受。在一部开创性的著作(1986)中,为了将单纯形转换到真实空间,Aitchison用一套基本原理发展了一种成分数据分析的公理方法。基于这些基本原理,Aitchison等人发展了各种方法、运算和工具,包括:
- 加性对数比(ALR)
- 中心对数比(CLR)
- 等距对数比(ILR)变换。
我们应该选择哪种转换?:这三种对数比变换之间的区别在于选择除数。换句话说,就是要选择使用哪个值来归一化样本中的所有值。每一次转型都有自己的弱点或优势。从理论上讲,ALR变换的一个缺点是,按照定义,变换在组成的部分是不对称的。因此,对于不同的因子,变换空间中的点之间的距离是不同的。因此,这意味着ALR转换后的数据不应该使用标准的统计方法,如方差分析和t检验,尽管如Aitchison所述,并在Aitchison等人中得到了进一步的发展。这一弱点是一个概念问题,而不是实际问题。ALR变换的主要缺点是:它不是从具有Aitchison度量的单纯形到具有普通欧氏度量的实ALR空间的等距变换。虽然在实加性对数比(ALR)空间中使用适当的斜坐标度量可以解决这一缺陷。然而,这并不是一种标准做法。在实践中,ALR转换或选择参考类群对解释结果相对简单,因为保留了与原始D-1第一部分的关系。这是ALR的优势所在。然而,可能并不总是有明显的参考可供选择,参考分类群的选择有点武断,结果可能会因参考的选择而有很大的不同。这可能是《用R分析成分数据》中没有将ALR变换用于成分数据分析的原因之一,尽管ALR函数是可以选择的。通过避免选择除数的ALR变换问题(例如,使用一个参考分类单元),CLR变换除以几何平均值。CLR的优点在于它是具有Aitchison度量的单纯形到具有普通欧氏度量的实空间的子空间上的等距变换。然而,缺点是CLR协方差矩阵是奇异的,这使得在没有适应的情况下很难在一些标准统计程序中使用。此外,其子空间中的正交参考不是以直接的方式获得的,这被认为是其突出的弱点。ILR避免了ALR的任意性和CLR的奇异性。它具有显著的概念优势;然而,原始成分和转换后的变量之间没有一对一的关系,很难解释结果。因此,在实践中,ILR在使用中的采用有限。
成分数据分析中如何处理零点:自20世纪80年代以来,成分数据分析的一个关键进展是使用对数比方法。然而,对数比法并没有解决零问题,而是强调了处理零的重要性。由于没有定义零的对数,对数和对数比转换需要数据矩阵中的非零元素;因此,成分数据分析之前必须先处理零。这三种对数比变换难以满足排序数据集的复杂性带来的核心挑战,特别是解决零问题。我们已经在第2章复习了零的话题,并将在第12章的零膨胀模型中进一步介绍此主题。这里我们回顾一下成分数据分析员是如何处理不同类型的零的。零是由许多复杂的原因造成的,目前没有简单的一般治疗策略。成分数据分析员试图找到潜在的原因,并确定要应用的适当方法。自从Aitchison提出了通过替换和使用模型来处理零的最初方法以来,在成分数据分析中已经发展了几种处理方法。
A 处理四舍五入的零:对于舍零,大多数方法将其视为一种特殊的NMAR(在随机不丢失)情况,并通过使用非参数乘法替换来处理它们和更复杂的基于模型的替换参数方法:用一个小的非零值替换它们。从技术上讲,四舍五入零点的非参数方法本质上是用推算来代替每个零点的一小部分;同时已经提出了几种四舍五入的组成零的策略。四舍五入零的参数方法之一使用普通期望最大化(EM)算法的修改并结合ALR变换来生成低于检测限值的适当估计。归零的目的是避免使用对数比变换取零的对数。然而,在实际研究中,很难用特定的小非零值替换零,同时不会扭曲统计估计,特别是在稀疏程度发生巨大变化和出现异常值的情况下。
B 处理采样零点问题:抽样零被认为是抽样过程的结果,而不是真正的零,需要专门的方法。为了解决抽样零问题,已经提出了结合Dirichlet分布的贝叶斯乘法(BM)处理。贝叶斯替换技术被认为是处理零计数的最流行的方法。Martín-Fernández等人提出了一种新的贝叶斯乘法成分数据分析方法。它涉及对零值的贝叶斯推断和对计数矢量中的非零值的乘法修改。零值被其后验贝叶斯估计所取代。以乘法方式修改非零部分。这一修改保留了各部分之间的原始比率,以及向量的总和表示,部分之间的关联略有扭曲。基于有价值的信息:成分向量的平均值等于其几何平均值、几何BM(GBM)先验和GBM替换。2015)是为了取代零。然而,尽管在贝叶斯替换技术中,GBM替换的效果最好,但是没有一种贝叶斯方法,无论是GBM替换,还是贝叶斯方法,都不能完全解释尺度不变性。因为它不完全符合成分数据分析的尺度不变性原则,研究人员对贝叶斯替代方法提出了进一步的质疑,并返回到直接使用基于模型的替换程序来计算低于检测限值的值,并开发了R软件来实现它。例如,此过程的一个版本当前在库“robComposition”(Bacon-shone 2003)的函数impRZilr()中实现。
C 处理结构零点问题:有各种尝试来解决结构性零问题。Aitchison and Kay和Bacon-shone专门针对这类零的治疗做出了相关贡献。虽然目前还没有处理结构性零点的通用方法,但很明显,应对结构性零点的策略用一个较小的值替换它是不合适的。在成分数据分析的框架下,早期的研究大多承担着判断零是否为结构性的责任。他们认为,结构性零可以出现在成分是连续变量或百分比的数据集中,也可以出现在计数数据的离散组合中,并分别基于二项条件Logistic正态模型和泊松-对数正态分布对它们进行建模。虽然这两种方法已经成功地模拟了结构零点,但是,结构零点问题是迄今为止最复杂的问题;它需要具体的模型来考虑组合零点和非零点成分。
综上所述,在成分数据分析框架下区分零源并基于不同类别(四舍五入、抽样或结构零)进行建模的方法存在困难、麻烦和挑战,特别是在组学研究领域。在经济学中,零的问题更为复杂,因为要将抽样零和结构零分开并不容易。微生物组读数是通过两种基于高通量测序的方法产生的:一种是通过对16SrRNA标记基因进行测序,另一种是鸟枪测序,即对样品中出现的所有微生物基因组进行测序。在获得测序读数之后,通过与一些已知的参考序列进行比对来量化数据,并将其归一化为相对丰度,以使成分数据具有可比性。一般来说,我们可以说,在数据生成的过程中会出现大量的零。然而,组成数据集中出现零值可能是由于多种不同的原因。零测量值的存在,要么是因为组件不存在,要么是因为它存在但没有取样,或者是因为发生了一些测量误差。
二、为什么微生物组数据集可以被视为成分?
微生物组数据集可以被视为成分的原因有几个。
微生物组数据集的结构是组成的:在他1986年的研讨会工作(Aitchison 1986)中,Aitchison总结出组成数据集有四个特征:(1)数据阵列的每一行对应于一个重复的、单一的实验或观察单元;(2)每列对应于每个组成的特定成分或部分;(3)每个条目是非负的;(4)每行条目的总和是1,或相当于100%。微生物组数据相对丰度表满足组成数据集的特征。
微生物组数据的相对值可能是微生物组研究的重点:在某些情况下,微生物组研究真正感兴趣的是比较不同成分的相对数量或相对丰度。也就是说,研究人员真正感兴趣的是不同组件的真正相对特征。例如,在肥胖微生物群研究中,研究兴趣之一是拟杆菌相对丰度与Firmicuts相对丰度的比率。在这种情况下,特定样本的总读取次数本身并不具有信息性或本身并不重要。
微生物组数据的来源可能会使数据的总值变得毫无意义:从测序的角度来看,从高通量测序生成的数据集是预定义的或被约束到某些常量。包括RNA测序(RNA-SEQ)、16S rRNA基因片段测序(Illumina HiSeq或454焦测序)、染色质免疫沉淀测序(CHIP-SEQ)、元基因组分析和选择性生长实验的组学数据集由映射到每个样本中的大量特征(例如,OTU、基因、物种或任何分类水平)的测序读数的计数组成。机器的容量(使用的测序平台)和在运行中多路复用的样本数量决定了观察到的读数(测序深度)。因此,虽然高通量测序方法报告的读数总数很大,但是有限。
样品制备限制微生物组数据仅携带相关信息:样品制备和DNA/RNA提取过程以确保数据只携带相关信息的方式对组学进行了测量。例如,RNA测序从固定重量或体积的组织样本开始,提取固定重量或体积的DNA/RNA,并从固定体积的总RNA中获得有限数量的序列片段读取。总之,从本质上讲,微生物组数据的共同特征是组成的基于Aitchison定义的标准。因此,成分数据分析方法可以应用于微生物组数据。
选择组合方法分析微生物组数据的实用规则:在实践中,我们如何判断组合方法是否合适?通常,当我们感兴趣的是它们成分之间的比率,而不是向量的总和,那么组合方法是合适的。特别地,数据的适当性成分数据的转换可以通过回答两个问题来解决。首先,这些数据的总数是否有用?第二,观察结果之间的绝对差异重要吗?当我们对这两个问题都回答“是”时,就意味着数据属于欧几里得空间,传统的统计方法是有效的。如果我们对这两个问题都回答否,这意味着数据属于Aitchison单纯形,必须在分析之前进行转换。大多数rna-seq分析工具,例如用于16SrRNA基因分析的主要工具(cheime,mothur和vegan)和chIP-seq分析工具,都假定数据集中的值是欧几里得的,绝对差异是重要的。
三、 Exploratory Compositional Data Analysis( 探索性成分数据分析)
① Compositional Biplot
成分双线图是探索多变量成分数据最广泛使用的工具之一。成分双标图被认为是在探索微生物组数据集时应该使用的第一个探索性数据分析工具。该图显示了样本是否被分成不同的组;哪些分类群推动了这种分离,哪些分类群与分析无关。在第一章。7、在介绍主成分分析(PCA)时使用的是双曲线图,但没有详细说明。在这里,我们将进一步介绍它的概念和用途。双曲线图由Gabriel提出,在同一曲线图中显示观测数据(对象或样本)和变量,以描述它们之间的联合关系。名称bilot中的前缀“bi”是指同时显示数据矩阵的行(观察值或样本)和列(变量),而不是指曲线图的二维性。二重图通常用于矩阵的图形显示,并将其应用于主成分分析(称为主成分二重图)。由于二维以上的显示通常很难制作,甚至更难解释,大多数双线图只显示数据矩阵中最大变化量的两个维度。
参考资料
