10.耿贝尔分布(Gumbel distribution)

Gumbel 分布（Generalized Extreme Value distribution Type-I）是一种极值型分布。举例而言，假设每次测量心率值为一个随机变量（服从某种指数族分布，如正态分布），每天测量10次心率并取最大的一个心率值作为当天的心率测量值。显然，每天纪录的心率值也是一个随机变量，并且它的概率分布即为 Gumbel 分布。

概率密度函数（PDF）

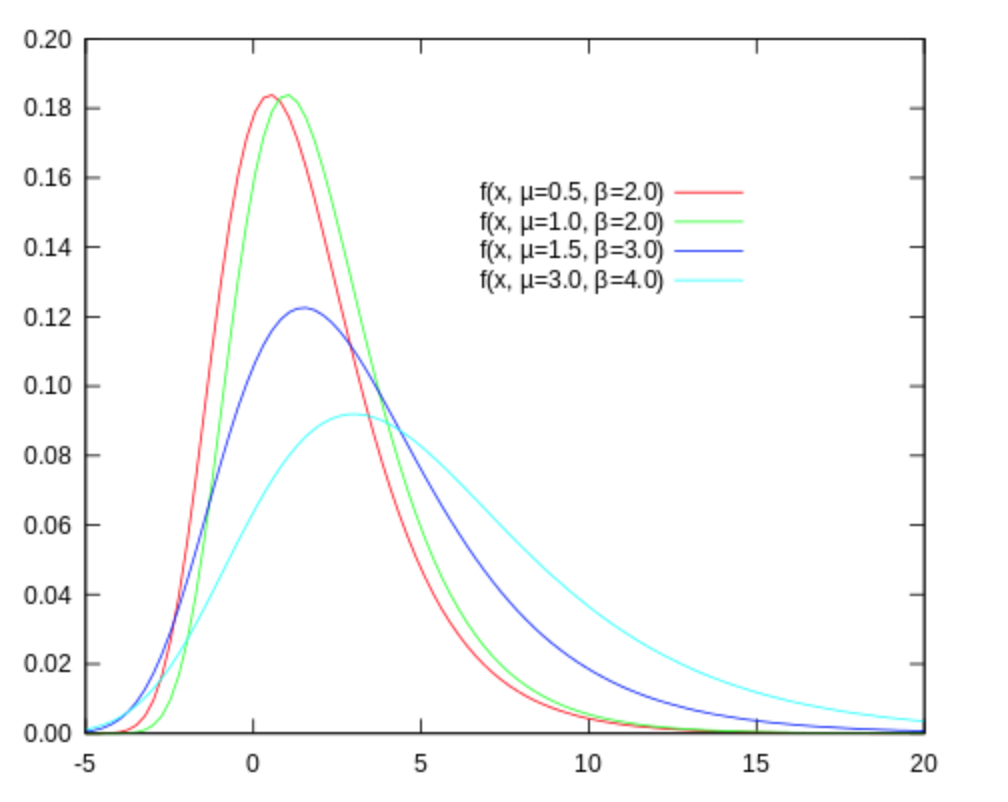
Gumbel 分布的 PDF 如下：

$$ f(x;μ,β) = e ^{-z-e^{-z}} , z= \frac{x-μ}{β}$$

公式中，μ 是位置系数（Gumbel 分布的众数是 μ），β 是尺度系数（Gumbel 分布的方差是

$$\frac{π^{2}}{6}β^{2}$$

def gumbel_pdf(x, mu=0, beta=1):
    z = (x - mu) / beta
    return np.exp(-z - np.exp(-z)) / beta

print(gumbel_pdf(0.5, 0.5, 2))

累计密度函数（CDF)

相应的，gumbel 分布的 CDF 的公式如下：

$$ f(x;μ,β) = e ^{-e^{-\frac{x-μ}{β }}} $$

def gumbel_cdf(x, mu=0, beta=1):
    z = (x - mu) / beta
    return np.exp(-np.exp(-z))

print(gumbel_cdf(5, 0.5, 2))

CDF 的反函数

根据 CDF 容易得到其反函数：

$$F^{-1}(y;μ,β) = μ- β ln(-ln(y))$$

我们可以利用反函数法和生成服从 Gumbel 分布的随机数。

def inv_gumbel_cdf(y, mu=0, beta=1, eps=1e-20):
    return mu - beta * np.log(-np.log(y + eps))

print(inv_gumbel_cdf(gumbel_cdf(5, 0.5, 2), 0.5, 2))

def sample_gumbel(shape):
    p = np.random.random(shape)
    return inv_gumbel_cdf(p)

print(sample_gumbel([2,3]))

此分布系根据极值定理导出，由费雪(R·A·Fisher ) 和蒂培特(L·H·C·Tippe -t t) 于1928 年发现各个样本的最大值分布将趋于三种极限形式种的一种，具体由型式参数K确定，当K=0的时候也就是耿贝尔分布，水文方面主要用第I 型渐近极值分布，是耿贝尔在1941年将此分布应用于洪水颁率分析工作，所以也称Fisher一Tippe 优工型分布。

这种算法在西方有些国家得到较为广泛的应用。目前耿贝尔分布被广泛运用于最大风速的计算当中

参考资料

• https://baike.baidu.com/item/%E8%80%BF%E8%B4%9D%E5%B0%94%E5%88%86%E5%B8%83/1381013?fr=aladdin
• https://blog.csdn.net/jackytintin/article/details/79364490
• https://en.wikipedia.org/wiki/Gumbel_distribution