8.t分布

一、t 分布的概念

在统计应用中，可以把任何一个均数为μ，标准差 为σ的正态分布N(μ , σ²)转变为 μ=0 σ=1的标准正态分 布，即将正态变量值X用Z = (X -μ)/σ 来代替。 由于$$\bar X$$ 服从正态分布，故 $$Z= {\frac{\bar X - \mu}{\sigma_{\bar X}}}$$ 服从标准正态分布N (0,1)。

实际资料的分析中，由于σ往往未知，故标准化转换演变为：

$${\frac{\bar X - \mu}{S_{\bar X}}} = {\frac{\bar X - \mu}{\frac{S}{\sqrt{n}}}} $$

服从v = n-1的t分布，即：

$$t= {\frac{\bar X - \mu}{S_{\bar X}}}$$

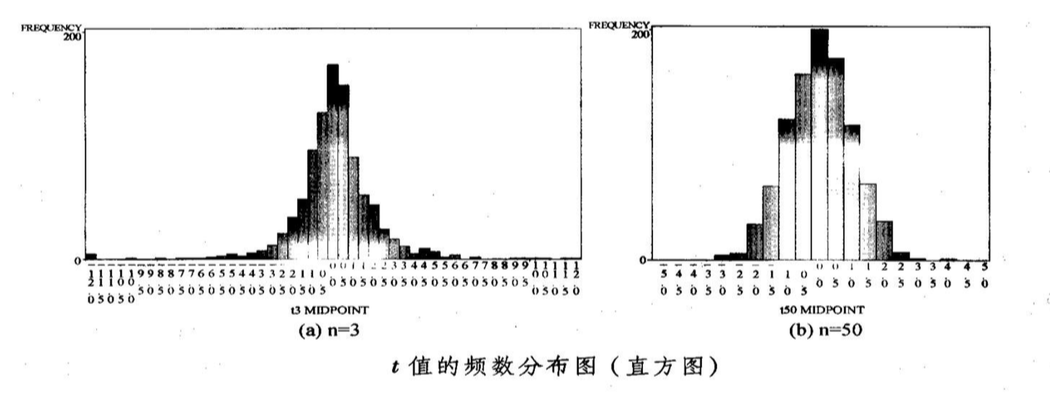
二、t分布曲线特点:

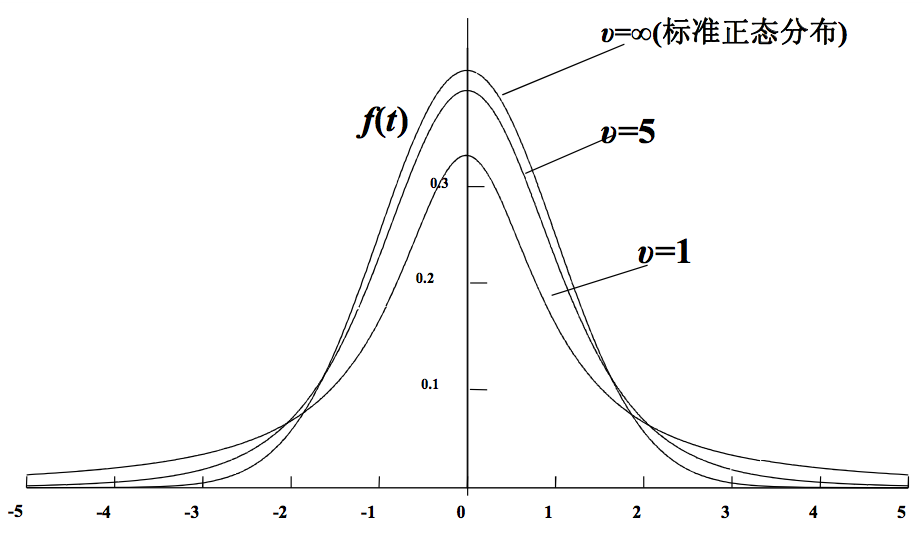
1. t 分布曲线是单峰分布，它以0为中心，左右对称。
2. t 分布的形状与样本例数 n 有关。自由度越小，则S_X 越大，t 值越分散，曲线的峰部越矮，尾部则偏高。
3. 当 n→∞时，则 S 逼近 σ，t 分布逼近标准正态分布。 t 分布不是一条曲线，而是一簇曲线。

三、正确使用 t 界值表

与单侧概率相对应的 t 值用 t（α ,n ) 表示，与双侧概率相对应的 t值用t(α/2,v) 表示。

由于 t 分布是以0为中心的对称分布，表中只列出了正值， 故查表时，不管 t 值正负只用绝对值表示。

讨论

T分布与正态分布曲线看上去很像，这里主要是因为T分布是为了小样本的数据分布，当自由度n趋于无穷大时，T分布曲线就越接近标准正态分布曲线

没有例子，对t分布的理解还是有些不到位呀。

参考资料

中山大学课程 《医学统计学》方积乾