【2.6】数据标准化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

一、数据标准化的原因

1.1 数据内部不同的差异程度

先来看看下面这样一个例子（例子来源：《医学统计学》）：

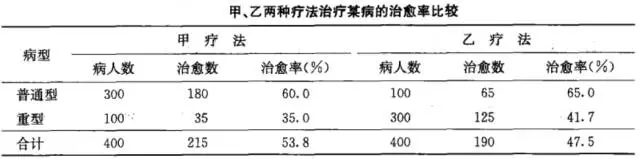
我们现在要比较甲、乙两种疗法哪一种对该病的治疗比较好。如果就像表里最后一行那样，你只是简单地算个总合，看治愈的总人数占总病人数的比例是多少，那么你立刻就能得到这样的数据：甲疗法的治愈率为53.8%，乙疗法的治愈率为47.5%，于是你就下结论了：甲疗法的效果比乙疗法的要好。

这种结论靠得住吗？咱们细细地看一下数据就会发现，病人是分两类的：普通型和重型。甲疗法中普通型的病人很多，而乙疗法中重型病人很多（常识告诉我们，普通小感冒肯定比重度流感要好治多了），这种差异就要求我们不能简单的看合计数据去下结论，比较前要先对把数据做点处理，让甲疗法与乙疗法的比较更加客观合理一些，对吧？

这里所说的“做点处理”就是指对数据的标准化！对于这种医学统计的数据，经常使用的标准化方法是用下面的公式计算：

$$ p' = \frac{\sum N_{i}p_{i}}{N} $$

其中N是总人数，Ni是每个类型的总人数，pi是每个类型的治愈率。这公式啥意思呢，是不是感觉开始晕了？没事，我来解释一下你就明白了：首先，咱们针对不同类型病人分开计算甲疗法和乙疗法各自的治愈率，然后我们假设这两种疗法要面对的两类病人的数量都是一样的，比如普通型和重型病人都是400人，再然后呢，用每种病人数400分别乘以各自的治愈率，是不是就可以得到两种疗法在相同病人基数的前提下可以分别治愈多少个普通型病人和多少个重型病人了呢？

标准化进行计算该数据的过程如下：

于是，数据标准化后显示乙疗法的效果其实是比甲疗法要好一些的。这与标准化之前的结果正好是相反的。通过这个例子，有没有感受到标准化的重要性了？

其实，对于统计学算法来说，是没法判断普通型病人好治一些还是重症病人好治一些，我们也很难客观地给一个权重说，治好一个重型病人比治好一个普通病人，对于疗法的评估来说要重要多少。而上面这种标准化方法是很通用的，它不用去管权重的问题，以及类型之间的差别到底有多大，它只需要很单纯地针对组内和组间数据做一个统一的处理，如果我们有N种疗法，针对N种病人，也是一样的标准化过程。

1.2 数据中不同特征或者变量之间具有不同的单位

还是来看一个例子（例子来源：《统计建模与R软件》）：

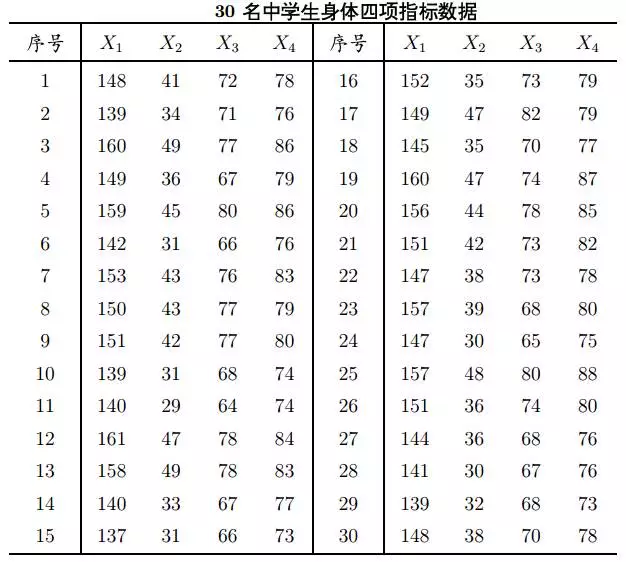
比如我们现在想对30名中学生的4项身体指标（X1：身高，X2：体重，X3：胸围，X4：坐高）进行聚类分析或者主成分分析。我们都知道体重的单位（kg）与其他3个变量的单位（cm）是不同的，若直接对数据进行计算，显然是不合理的，因为谁也没法告诉你“1 kg + 1 cm”到底等于什么！

遇到这样的情况，通常的做法就是通过标准化方法，将单位相同的值做除法，消除它们的单位，然后再通过一些必要的转化，最终可以将不同单位的变量进行比较，或者做其它的分析处理。

二、数据的标准化的方法（Normalization Method）

其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上，常见的数据归一化的方法有：

2.1 min-max标准化(Min-max normalization)

也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下：

x=(x-Xmin)(Xmax-Xmin)

其中max为样本数据的最大值，min为样本数据的最小值。这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

2.2 log函数转换

通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

x=log10(x)/log10(max)

看了下网上很多介绍都是x*=log10(x)，其实是有问题的，这个结果并非一定落到[0,1]区间上，应该还要除以log10(max)，max为样本数据最大值，并且所有的数据都要大于等于1。

2.3 atan函数转换

用反正切函数也可以实现数据的归一化：

x=atan(x)*2/π

使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上。

2.4 z-score 标准化(zero-mean normalization)

也叫标准差标准化，经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：

x=(x-μ)/σ

其中μ为所有样本数据的均值，σ为所有样本数据的标准差。 而并非所有数据标准化的结果都映射到[0,1]区间上，其中最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法

datascale<-scale(data_read,center=T,scale=T)

2.5 中位数标准化

先来解释下中位数（Median），它表示一组数据中数值刚好在最中间的那个值，这个值可将数值集合划分为相等的上下两部分。比如说下面一个数列：

1，3，4，6，7，8，10

中位数就是6，它把数列分成比6小的三个数，和比6大的三个数。如果数列中数值是偶数个，那么中位数就等于最中间两个值的平均值。

我们很容易看出来，中位数不受数列的极大值或极小值影响，所以它对数列有很好的代表性。

中位数标准化，就是将每一个数据除以对应列的中位数（median），R语言代码如下：

>datamedian<-sweep(data_read,2,apply(data_read,2,median,na.rm=T),FUN="/")

首先我们用apply函数求出每一列的中位数，然后用sweep函数横扫整个数据，将每一个数据除以对应列的中位数，得到最后的结果。

2.6 均值标准化

均值大家都很熟悉了，就是通常说的平均值。均值标准化就是将每一个数据除以对应列的均值（mean），用R实现如下：

>datamean<-sweep(data_read,2,apply(data_read,2,mean,na.rm=T）,FUN=“/”)

首先我们用apply函数求出每一列的中均值，然后用sweep函数横扫整个数据，将每一个数据除以对应列的均值，得到最后的结果。

2.7 总和标准化

该方法就是将每一个数据除以对应列的总和（sum），R代码如下：

>datasum<-sweep(data_read,2,apply(data_read,2,sum,na.rm=T),FUN="/")

首先我们用apply函数求出每一列的总和，然后用sweep函数横扫整个数据，将每一个数据除以对应列的总和，得到最后的结果。

2.8 中心化

该方法就是将每一个数据减去对应列的均值，数据变换后，均值为0，方差不变。中心化以后，由于数据的均值变成0，可以消除量纲、数据自身差异所带来的影响（此处是做减法而不是除法，所以变量的单位还是保留的），而且对线性回归以及模型预测方面也有好处，具体的解释本文就不展开的，感兴趣的小伙伴们可以参考以下的资料：http://www.theanalysisfactor.com/center-on-the-mean/。

R代码如下：

>datameancenter<-sweep(data_read,2,apply(data_read,2,mean,na,rm=T),FUN="-")

首先我们用apply函数求出每一列的均值，然后用sweep函数横扫整个数据，将每一个数据减去对应列的均值，得到最后的结果。

亦或是直接使用scale函数：

>datameancenter<-scale(data_read,center=T,scale=F)

2.9极差标准化

该方法就是将每一个数据（xij）减去对应列的均值(）

然后除以对应列最大值与最小值之间的差值（Rj），公式如下：

R代码如下：

>datacenter<-sweep(data_read,2,apply(data_read,2,mean,na.rm=T),FUN="-")
>daraR<-apply(data_read,2,max,na.rm=T)-apply(data_read,2,min,na.rm=T)
>datameanR<-sweep(datacenter,2,dataR,FUN="/")

第一步先求出分子，第二步求出分母，最后将二者相除即可。

二、python实现

1、(0,1)标准化：

这是最简单也是最容易想到的方法，通过遍历feature vector里的每一个数据，将Max和Min的记录下来，并通过Max-Min作为基数（即Min=0，Max=1）进行数据的归一化处理： Python实现：

def MaxMinNormalization(x,Max,Min): 
 x = (x - Min) / (Max - Min); 
 return x;

找大小的方法直接用np.max()和np.min()就行了，尽量不要用python内建的max()和min()，除非你喜欢用List管理数字偷笑。（np为import numpy as np）

2、Z-score标准化：

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，这里的关键在于复合标准正态分布，个人认为在一定程度上改变了特征的分布，关于使用经验上欢迎讨论，我对这种标准化不是非常地熟悉， Python实现：

def Z_ScoreNormalization(x,mu,sigma): 
 x = (x - mu) / sigma; 
 return x;

这里一样，mu（即均值）用np.average()，sigma（即标准差）用np.std()即可。

参考资料

• http://www.itongji.cn/article/111313422012.html
• http://blog.csdn.net/kryolith/article/details/39770187
• https://mp.weixin.qq.com/s?__biz=MzI3MTM3OTExNQ==&mid=2247484001&idx=1&sn=baa929603032f6027719d8134380bea0&chksm=eac3fda5ddb474b3247172f6d943bdc4f9ded2dda77e57dc58930589121ab23b635e347941da&scene=21#wechat_redirect