【4.7.3.8】结构比较--LDDT
LDDT 的全称是 local distance difference test,局部距离差测试,在它被提出来的时候也不是全新概念,它来自 dRMSD + GDT。
dRMSD(distance RMSD)是 RMSD 的变体,计算每一个分子内部原子对的距离,再考虑2个分子的对应的原子对的距离差 [12]。也就是说,RMSD 计算的是两个分子对应原子的距离差(在重叠对齐后),dRMSD 计算的是两个分子对应原子对的距离差的差值(公式17)。dRMSD 的最大的特点是:它的计算不依赖于将两个结构重叠对齐!
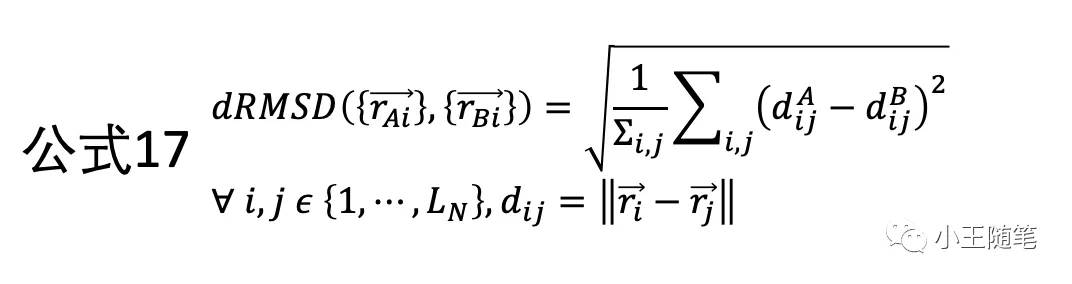
2010年,CASP9,Mariani 等人在评估基于模板的预测结构时引入了 DDT(distance difference test)[13-14]。作者将 DDT 视为 dRMSD equivalent of GDT。
dRMSD + GDT —> LDDT
GDT 是两个分子重叠后小于预设距离阈值的残基数与残基总数的比值。DDT 是小于预设距离阈值的分子内距离对的数目与距离对总数的比值。
Mariani 等人在2013年正式推出 LDDT 的论文中并没有给出数学公式,仅有文字描述,甚至不是伪代码算法;Senior 等人在 AlphaFold1 的论文的补充材料给出了一个公式(公式18)[15]。因为 AlphaFold1 是在王晟和导师许锦波的以接触图+ResNet的框架下的改进,而其改进之一是用距离图(distogram)取代接触图,所以仿照 LDDT 定义了 distogram LDDT,即 DLDDT(公式19)。
很快,依旧沿着王-许方法的路径,杨建益和导师 Baker 用取向图(orientogram)取代了距离图;紧接着,CASP14 中,AlphaFold2 另辟蹊径,使用了完全不同的深度学习框架。可以预见,distogram 与 DLDDT 都将与过去的许多度量一样,成为历史名词。
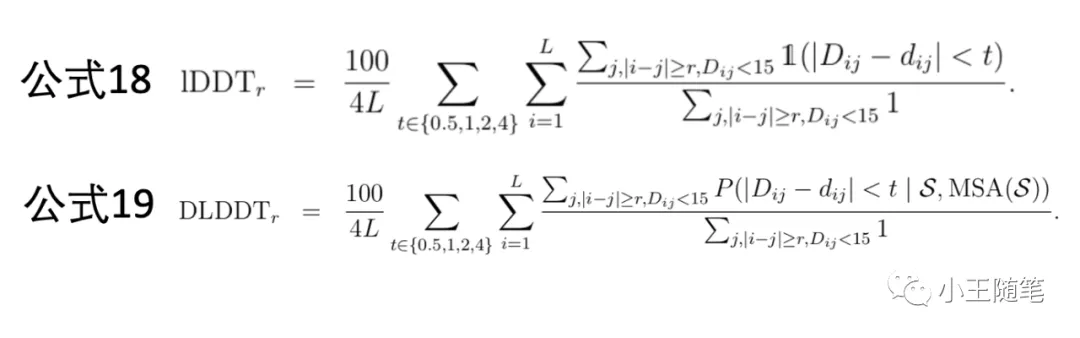
就公式18我们解释一下 LDDT 的含义:
考虑天然结构内的原子之间的距离 Dij,需要 Dij > 15 Å 且 |i - j| ≥ r,由此得到符合条件的原子对 (i, j)。这时考虑预测结构内这些原子对的距离 dij,如果 |Dij - dij| < tolerance,则加1。分别令 tolerance = 0.5, 1, 2, 4 Å,计算满足条件的距离差的比例,再取均值。
如果 tolerance 很小,那么意味着满足 |Dij - dij| < tolerance 的原子对 (i, j) 在天然结构和预测结构中的距离几乎一致。
从另一个角度看,无论 tolerance 预设为何值,满足条件的原子对 (i, j) 越多,说明在此容忍度下,预测结构与天然结构内部原子之间的距离越一致,那么两个结构应当越相似。—— 通过计算预测结构的内禀距离判别是否与天然结构相似。
由此,在 AlphaFold2 中,Jumper 等人设计了pLDDT,per-residue LDDT,通过计算预测结构的内禀距离,在缺乏天然结构的情况下,判断预测结构中的每一个残基的可信度。[1]

利用 predicted pLDDT 进行预测精度的自评估是 AphaFold2 正文列举的7大创新之一。
实际上,细读 AlphaFold2 论文可以看到,predicted pLDDT 并非作者的首选。—— 信息熵才是。信息熵的基本思想就是比较两个结构的内禀距离的概率分布的差异,与 LDDT 的基本想法是一样的。

参考资料
