【6.4.2】Tango预测蛋白聚集区域
TANGO算法使用的模型旨在预测肽和变性蛋白质中的交叉β聚集(cross-beta aggregation),并由一个包含随机coil和4种可能结构状态:β转角,α螺旋,β折叠和 α-螺旋聚集,组成相空间( phase-space)。 肽的每个片段都可以根据玻耳兹曼(Boltzmann)分布来填充这些状态中的每个状态,即,给定片段的每个结构状态的总体频率将与其能量有关。 因此,预测肽的跨β聚合片段,TANGO只需计算相空间的分配函数即可。
官网: http://tango.crg.es/about.jsp
一、软件介绍
在这里,我们首先描述如何确定每种不同结构状态的倾向性,如何对相空间进行采样以及在这些选择中嵌入哪些假设。 接下来,我们将讨论TANGO如何处理一组由21种蛋白质衍生的176种肽。
1.1 不同结构倾向性
1.1.1 阿尔帕螺旋倾向 Alpa-Helical propensities
最新版本的AGADIR(AGADIR-1s11)中使用的参数已用于确定氨基酸序列的螺旋倾向。 唯一的修改是两个窗口近似的实现(请参见下文)。
1.1.2 β-转弯倾向 beta-Turn propensities
通过考虑以下四个能量贡献来计算β转向倾向:
- 构象熵的氨基酸特定成本,用于将残基固定在β-turn相容构象(compatible conformation)中;
- 在特定位置,每个氨基酸与氨基酸结构中的转向结构相互作用
- 在某些情况下,转弯内的侧链-侧链或侧链-主链相互作用
- 转弯残基i和i + 3的主链之间的单个H键
我们仅考虑了可以获取大量统计数据的四种类型的转弯类型I,I,II和II。如先前所公开的,已经使用统计f,y矩阵获得了将特定氨基酸反过来固定为二面角的熵成本。由于残基i和i + 3可能采用不同的构象,并且依次不固定,因此我们在298K上应用0.3 Kcal / mol的一般熵惩罚项。氨基酸与转角的相互作用已通过蛋白质数据库的统计分析获得(请参见方法部分),假设观察到的相互作用计数高于预期值表示有利的相互作用,反之亦然。
1.2 交叉Beta聚合 Cross beta-aggregation
为了估计特定氨基酸序列的聚集趋势,我们采取以下假设:
- 在有序的β-折叠聚集物中,主要二级结构为β-链。
- 聚集过程涉及的区域被完全掩埋,从而支付了全部溶剂化成本和收益,完全熵并优化了其H键势(总数中形成的H键的数量与受主补偿的供体基团的数量有关)。 过多的捐助者或接受者仍然不满意。
- 所选窗口中的互补电荷建立了良好的静电相互作用,使肽的总净电荷和聚集区域附近的净电荷(在所选窗口之前或之后有两个
1.2.1 β倾向的估计
我们已经包括了三个能量贡献:用于将残基固定在β链构象中的构象熵的残基特定成本,以及残基i与位置i + 1和i + 2处的残基的侧链-侧链相互作用。
通常,与形成等长长度的α-螺旋相比,形成β-链所需的构象熵代价更少,因为Ramachandran图的β-链区域比α-螺旋区域大,而能量深度well是相似的( depth of the energy well is similar)。另一方面,单个β链不具有抵消构象熵损失的主链-主链氢键。在没有其他贡献的情况下,将不会在随机coil上填充β链。然而,通常不考虑的因素是链内侧链-侧链相互作用的存在,当有利时可以促进β-链群体。在空间上以扩展构象(β链)紧密结合的独特侧链是位置i和i + 2之间的那些侧链。 i和i + 1位置的残基也可能影响β链的形成,因为它们的平均距离比随机coil中的距离更远。这种现象具有充满活力的含义,我们称之为(i,i + 1)β-相互作用。在此基础上,有利的(i,i + 1)b相互作用反映残基i和i + 1之间的排斥,而(i,i + 1)β不利相互作用反映这些侧链不在β中时的吸引力-链构象。这些侧链-侧链相互作用在b-strand-coil过渡中引入了能量耦合,产生了一些协同性。
如先前所公开的,已经使用统计f,y矩阵获得了将特定氨基酸固定在β二面角中的熵成本。
参与方程式的其他两个项,残基i,i + 1和i + 2之间的相互作用,与侧链-侧链相互作用的能量贡献有关。它们是使用平均力势确定的。
1.2.2 聚集段的去溶剂化成本 Desolvation costs of aggregated segments
如上所述,我们假设构成有序聚集体核心的残基必须完全掩埋。这意味着完全去溶剂化和最小的自由度。掩埋序列拉伸的能量消耗由以下方程式定义:
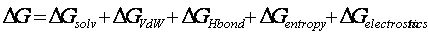
Dsolv和Dvdw是从FOLD-EF力场(参考)中获得的,假定最大埋葬量。 DHbond等于埋入链段产生的H键的数量乘以H键的贡献(在AGADIR1中使用相同的值)。 H键的数目等于多肽链中可以分别与受体或供体配对的供体或受体的数目。对于主链而言,每个残基始终为2,对于侧链,我们仅计算供体和受体的总数,并取两者中的最小值。对于Pro,我们认为,如果在段的N末端,则仅会丢失一个主链H键,而如果在C末端,则会丢失两个。段内的Pro会受到10 Kcal / mol的罚款。 熵假设全部熵成本,并且是由于残基处于扩展构象和侧链熵(如ABGYAN所述)而导致的主链熵之和。先前在Viguera,Lacroix,Serrano)中描述了用于计算静电对螺旋稳定性的贡献的模型。在下面的段落中,我们描述了如何计算β-聚集体的静电贡献。
1.2.3 静电的贡献 Electrostatic contribution
静电相互作用显然随电离度而变化,并因此随溶液的pH值而变化,而肽中可电离基团的pKa随静电环境而从其标准值变化。在TANGO中,我们考虑了所有静电相互作用(这涉及带电荷的侧链基团,游离的N端和C端主链基团,以及如果肽是琥珀酰化的琥珀酰保护基),以计算随机氨基酸的静电环境考虑到离子强度,温度和pKa(请参见下文),将coil和helical段分开。
TANGO区分了考虑中的段中的电荷(内部电荷)(被认为是完全掩埋的),该段的N或C端之外的被认为是溶剂暴露的两个残基中的电荷(相邻电荷),多肽链中的其余电荷(外部电荷)。外部电荷也被认为是溶剂暴露的,但是它们的贡献可以通过链长来校正。对于埋电荷,我们使用(332 /(8.8 * exp(-0.004314 *(temp-273.0))))的介电常数,而对于裸露电荷,则为332 /(88 * exp(-0.004314 *(temp-273.0)) ))。 假设所考虑的片段加上其相邻残基的净电荷,假设电荷之间的平均距离总计约为5A。对于其余的多肽链,TANGO会计算净电荷并将其除以为更长的多肽链引入较高平均距离的残基数。
静电相互作用有两种类型:由于净电荷引起的排斥相互作用和由于补偿电荷引起的吸引相互作用。引入后者是为了反映平均而言,某些补偿电荷将构成盐桥,从而有助于骨架的稳定性。在有吸引力的补偿电荷的情况下,我们校正通过将其除以3得出的有利的静电相互作用。引入了任意校正因子,因为如上所述,该术语反映了内部盐桥的形成,当然不能由所有补偿电荷形成。
1.3 alpha-Helix聚合
一些肽和蛋白质以螺旋构象聚集。 通常在倾向于形成卷曲螺旋结构或Leu拉链的蛋白质中观察到这一点(参考文献)。 由于二聚体或更高阶螺旋聚集体的形成将与β-折叠聚集体竞争,因此我们已以非常简单的方式将这种结构状态包含在TANGO算法中。 至于β-折叠聚集,我们假定聚集时完全埋葬,但仅针对螺旋结构的一个面。 因此,我们假设在螺旋状聚集体中,i,i + 1,i + 4,i + 5,i + 8,i + 9等残基将被完全掩埋。 对于这些残基,我们采用与掩埋β-sheet聚集体中的残基相同的考虑因素。 但是,将片段折叠成螺旋构象所需的能量直接来自AGADIR。
1.4 理化条件对聚集的影响
1.4.1 pH,离子和温度依赖性
如AGADIR2-1s11中所述,考虑了pH,温度和离子强度对静电相互作用的影响。类似地,如AGADIR2-1s11中所述,考虑了熵,氢键和疏水相互作用对温度和离子强度的依赖性。
1.4.2 TFE依赖
已经以下列方式考虑了TFE对此处考虑的不同结构构象的稳定性的影响。首先,我们假设H键对螺旋,转向和聚集构象的能量的贡献普遍增加(请参见BLANCO和SERRANO中的参考文献,PROT G)。其次,基于鲍德温及其同事的实验结果,我们考虑了氨基酸的螺旋性质的变化。我们认为,如果不考虑进一步的变化,TFE的作用与浓度高达40%呈线性关系。这是基于经验观察得出的,对于实验分析的许多肽,如果超过40%,则几乎没有变化。
1.5 通过两个窗口近似进行构象采样
理想情况下,要计算分区函数,如AGADIRms算法所用并在Munoz等人(2003年)中描述的多窗口近似。应该已经实施了。但是,由于我们考虑了4种可能的结构状态,因此分区函数的计算在计算上将过于苛刻。因此,我们选择了两窗口近似,它假设在同一条多肽链中发现两个以上有序片段的可能性太低而无法考虑(对于一个具有50个以上残基的肽段,一个简单的窗口将与现实相差太大)。我们的假设是,在同一条多肽链中,可能存在一个或两个非重叠(由5个非结构化残基或更多个残基分隔,请参见Munoz&Serrano,Biopolymers,AGADIR2-1s)结构化的片段。因此,这种简化可能会导致包含几个强烈预测的结构化区域的大蛋白出现偏差。
第二个简化是我们不考虑聚合中间体。为了简化分配功能,我们再次将聚集体视为与b-turn和a-螺旋构象竞争的单个分子物种或结构状态。可以假定聚集段具有无限的集中度,换句话说,即一旦形成聚集段,则立即以无限的缔合常数聚集,从而可以简化此简化过程。由于实际上聚集动力学和聚集程度将取决于肽的浓度及其缔合常数,因此这意味着我们获得的聚集概率只是相对的。因此,它们允许在同一多肽链内部进行比较,或与多肽链的突变体进行比较,但不能在不同多肽链之间进行比较。
第三,就像在AGADIR的多窗口近似中一样,我们假设在同一分子中同时存在的两个不重叠的片段(不依赖于它们的构象)之间没有能量耦合。对于没有长程或中程相互作用的单体肽,该假设似乎是相当合理的。最后,我们假设所有可能的状态可以成对共存于同一多肽分子中,即一个聚集体可以具有一个螺旋段,只要它不在聚集段中即可(有实验证据,如溶菌酶呈螺旋状)区域仍然存在于淀粉样蛋白聚集体中(DOBSON)。
在这些假设下,以及将随机coil状态定义为非螺旋,不转弯或不参与聚集的构象,两窗口序列分配函数成为结构化段所有可能组合的统计权重之和(来自一到两个非重叠的片段)加上随机coil状态的统计权重(不包括任何结构化片段的分子构象集)。随机coil的权重为1(来自随机coil状态下所有残差的权重的乘积)。作为第三个假设的结果,具有多个结构化链段的分子构象的统计权重仅仅是其上包含的所有结构化链段的权重的乘积(参见Munoz等人)。
二、下载安装
需要学术邮箱注册才可以下载安装
输入文件格式example.txt:
sup2 N N 7 298 0.1 AMAPVLYLQDKSS
sup2 N N 7 298 0.1 AMASVLYLQDKSS
sup2 N N 7 298 0.1 AMAPVLYLQSKSS
sup2 N N 7 298 0.1 AMASVLYLQSKSS
输入解释:
* 每一列的含义 "name Nterm-protected Cterm-protected pH Temperature Ionic Sequence"
* 第一列为序列的名字,输出文件也是用这个名字命名
* 输入序列最长为500 character,不要超过10条序列
* pH (0 - 12)
* Temperature [K] (273 - 400)
* Ionic strength [M] (0 - 5)
Concentration [M] (0.00001 - 5)
运行程序
tango_x86_64_release -inputfile=example.txt
参考资料
