【8.2】Kaplan–Meier方法
不错的资料:
一、方法介绍
该方法是由Kaplan和Meier于1958年共同提出的。我们首先通过一个例子对该方法进行理解:
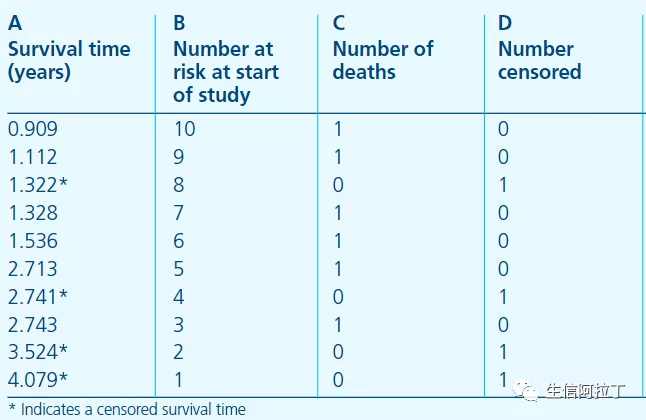
- A列是从试验开始起,持续的观测时间,星号代表在该时间有删失数据发生;
- B列是指在A列对应的时间开始之前所有存活的研究对象个数,也可以叫做at risk的人数,表示当前具有死亡风险的有效人群,是排除了已经死亡和删失的数据之后剩余的人数;
- C列为恰好在A列对应的时间死亡的人数;
- D列是在该时间点删失的个数,即在实验过程中丢失的、失去跟踪的数据。
在引入Kaplan–Meier公式之前,大家可以先尝试自己去思考下如何计算每个时间节点的生存概率,即研究对象从试验开始直到某个特定时间点仍然存活的概率S(t)。比如在1.536年这个时间点,即表中的第五行,病人在该点的生存概率是多少呢?
很容易可以想到,要想在1.536这个时间点存活,他/她必须在1.536之前的所有时间点存活才行,也就是说在0.909、1.112、1.322、1.328这几个时间点,病人都必须存活。那么在1.536这个时间点的生存概率实际上就等于在包括1.536 在内的所有之前的时间点都不死亡的概率乘积,即:P(存活至1.536) = P(0.909时不死亡) * P(1.112时不死亡) * P(1.322时不死亡) * P(1.328时不死亡) * P(1.536时不死亡)
对于某个特定时间点不死亡的概率,可以用 1 – 死亡概率 来估算,举个例子:P(0.909时不死亡) = 1 – P(0.909时死亡) = 1 – (0.909时死亡的人数)/(0.909之前的所有人数) = 1 – 1/10 = 0.9
当我们计算出每个时间点不死亡的概率之后,我们就可以通过连续乘积算出每个时间点的生存概率,即存活至该时间点的概率。如下表所示:
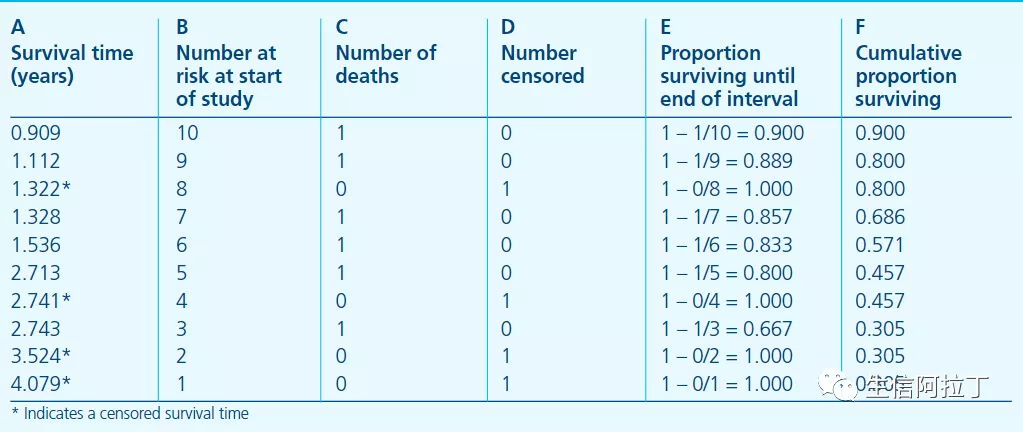
该表中E列即不死亡概率,F列则表示累积的生存概率,可以看到随着时间增加,死亡人数增多,越到后期,生存概率越低。
二、方法思路
上面这个例子的思路就是Kaplan–Meier方法的主要思路,我们也可以用数学公式来表示。一共有m个时间点,每个时间点用下标 i 来表示, i 为从 1 到 m 的整数, 生存概率 S(ti) 可以表示为:
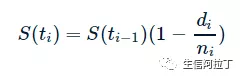
其中,ti 表示第 i 个时间点,ni 表示在 ti 之前的有效人数,di 表示在 ti 死亡的人数,S(ti-1) 表示在上一个时间点 i-1 的生存概率。
根据这一公式,我们可以画图来展示生存率的变化情况,即Kaplan-Meier生存曲线,如下图所示:

图中横轴即时间轴,纵轴是累积存活比例,也就是生存概率,加号表示删失数据。
三、差异检验
一般来说,生存分析是要比较不同组之间的一个生存情况,因此Kaplan-Meier生存曲线一般不止一条曲线。如果想比较整体生存时间分布是否存在统计学差异,一般我们可以采用Logrank统计方法来对生存数据进行统计分析。Logrank统计方法假设两组的生存时间分布一致,去检验是否能拒绝该假设。
除了Logrank检验之外,常用的检验包括Breslow检验,即Wilcoxon检验。该方法加入了权重因子,即每个时刻的总人数,使得试验前期的权重较大,贡献更大,所以Breslow检验对试验前期的差异更加敏感。
- Kaplan-Meier生存分析中三种检验方法(log-rank、 breslow 、 tarone )的比较
- log-rank法侧重于远期差别,breslow法侧重于近期差别,tarone法介于两者之间。
参考资料
