Information content(信息量)
在信息论中,信息内容、自我信息、惊奇信息或香农信息(information content, self-information, surprisal, or Shannon information)是从随机变量中特定事件发生的概率导出的基本量。它可以被认为是表达概率的另一种方式,很像odds或log-odds,但它在信息论的设置中具有特殊的数学优势。
香农信息(Shannon information)可以解释为量化特定结果的“惊喜”程度。由于它是这样一个基本量,它也出现在其他几种设置中,例如在给定随机变量的最佳源编码的情况下传输事件所需的消息长度。
香农信息与信息论熵密切相关,熵是随机变量自我信息的期望值,量化随机变量“平均”的惊人程度。这是观察者在测量随机变量时期望获得的关于随机变量的平均自我信息量。[1]
信息内容(information content)可以用各种信息单位来表示,其中最常见的是“位”(bit,有时也称为“香农”,shannon),如下所述。
一、定义
选择 Claude Shannon对自我信息(self-information)的定义是为了满足几个公理:
- 概率为 100% 的事件完全不足为奇,并且不会产生任何信息。
- 一个事件发生的可能性越小,它就越令人惊讶,它产生的信息也就越多。
- 如果分别测量两个独立事件,则信息总量为单个事件的自信息量之和。
详细推导如下,但可以证明存在满足这三个公理的唯一概率函数,最多可达乘法缩放因子。大体上给定一个事件 X有概率 P,信息内容定义如下:
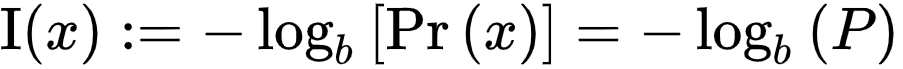
LOG的基数未指定,这对应于上面的比例因子。不同的基数选择对应不同的信息单位:对数底数为2时,单位为bit或shannon;如果对数是自然对数(以e 为底),则单位是nat,“natural”的缩写;如果基数为 10,则单位为hartleys、十进制 数字或偶尔为 dits
形式上,给定一个随机变量 X带概率质量函数px(x), 测量的自我信息(self-information ) X作为结果 X定义为

随机变量的香农熵X以上定义为
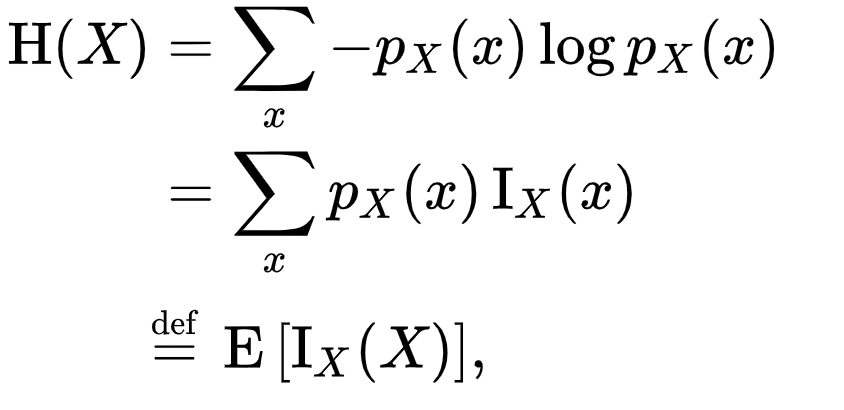
根据定义等于测量的预期信息内容X
记号的使用 Ix(x)因为上面的自我信息不是万能的。由于记号Ix(X)也常用于互信息的相关数量,许多作者使用小写 hx(x) 取而代之的是自熵,反映资本的使用 H(X) 为熵。
三、Properties(内容)
Antitonicity for probability(反序性的概率)
对于给定的概率空间,测量更罕见的事件将产生比更常见的值更多的信息内容。因此,在观察事件的概率中,自我信息是反补的。
直观地说,更多的信息是从观察一个意想不到的事件中获得的——它是“令人惊讶的”。
例如,如果Alice中彩票的概率是百万分之一,那么她的朋友Bob从了解到她中了彩票得到的信息要比她在某一天中输掉的信息多得多。(参见:彩票数学。)
这就建立了随机变量的自信息与其方差之间的隐式关系。
Additivity of independent events(独立事件的可加性)
两个独立事件的信息内容是每个事件的信息内容之和。这个性质在数学上被称为加和性,尤其是在测度和概率论中。考虑两个独立的随机变量X,分别具有概率质量函数pX(X)和pY(y)。联合概率质量函数为

可能性的对应属性是对数可能性独立事件的概率是每个事件的对数概率之和。将对数可能性解释为“支持”或“负面惊喜”(the事件支持给定模型的程度:模型由某一事件在某种程度上是不令人惊讶的,这说明独立事件添加了支持:信息这两个事件一起提供了统计推断它们的独立信息之和。
参考资料
